Предмет: Алгебра,
автор: belka003
решите систему неравенств: {2(cos^2x-sin^2x) >=1;
sin2x<корень из 2 на 2 .
Приложения:

Ответы
Автор ответа:
2
По формуле косинуса двойного угла: cos2a = cos²a - sin²a, получим
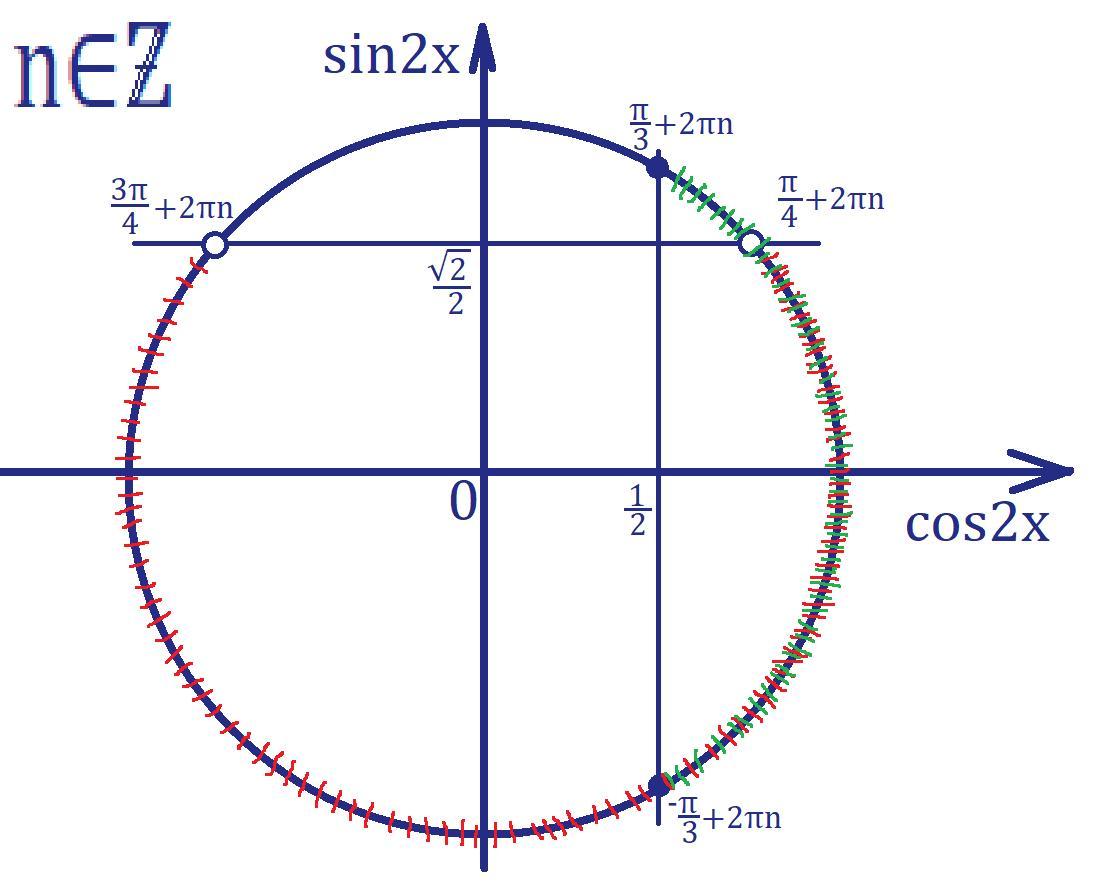
Решим систему на тригонометрическом круге, смотри внизу.
Ответ:
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: girlverycool6174
Предмет: Математика,
автор: samsonova2010kat71
Предмет: Математика,
автор: kostylevaana22
Предмет: Математика,
автор: аомоаооаослалал
Предмет: История,
автор: xbox360ps2ps3ps