Предмет: Математика,
автор: mufate
найдите tg2a если sina=12/13, пи/2<a<пи
Приложения:
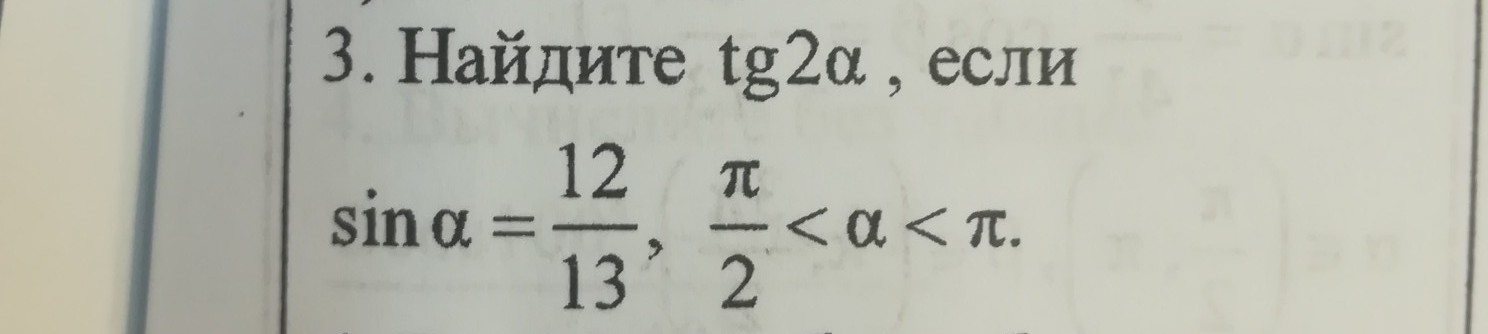
Ответы
Автор ответа:
4
Похожие вопросы