Question

построить график функции y = √4x и найти:
1) y(9)
2) значение x, при котором значение функции равно 20
3) промежуток, на котором функция принимает положительные значения
4) промежуток, на котором функция возрастает

Answer 1

Ответ:

Дана функция $\tt \displaystyle y=\sqrt{4 \cdot x}$ .

а) Область определения функции: 4·x≥0 ⇔ x≥0 ⇔ D(y)∈[0; +∞).

б) Множество значений: $\tt \displaystyle \sqrt{4 \cdot x}\geq 0$, поэтому E(y)∈[0; +∞).

в) нули функции: y=0 ⇔ $\tt \displaystyle \sqrt{4 \cdot x}=0$ ⇔ x=0.

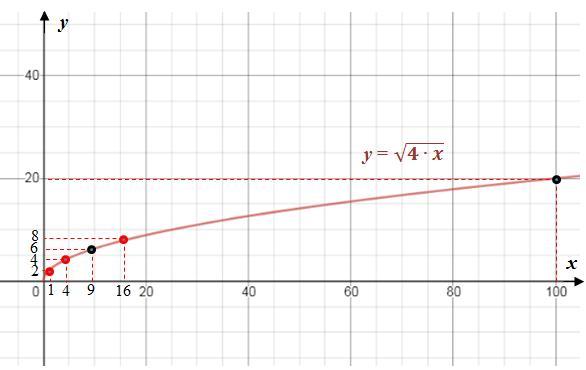
г) определим несколько значений функций (красные точки):

y(1)=$\tt \displaystyle \sqrt{4 \cdot 1}=\sqrt{4}$ =2;

y(4)=$\tt \displaystyle \sqrt{4 \cdot 4}=\sqrt{4^2}$ = 4;

y(16)=$\tt \displaystyle \sqrt{4 \cdot 16}=\sqrt{64}=\sqrt{8^2}$ =8.

Рисунок в приложении.

1) y(9)= 6 (чёрная точка);

2) y(x)= 20 ⇔ x =100 (чёрная точка);

3) Из рисунка видно, что функция принимает положительные значения на промежутке (0; +∞);

4) Из рисунка видно, что функция возрастает на промежутке (0; +∞).