есть кто-нибудь, кто разбирается в параметрах? помогите, пожалуйста разобраться с двумя номерами (:

Ответы
213. Построим график функции . Посмотрим, как раскрываются модули в зависимости от значения x. Для этого представим:
,
. Отметим на числовой прямой нули подмодульных выражений и рассмотрим все варианты раскрытия (первый модуль - левый знак, второй модуль - правый знак). Знаки указаны на рис. 1. Тогда функция принимает вид:
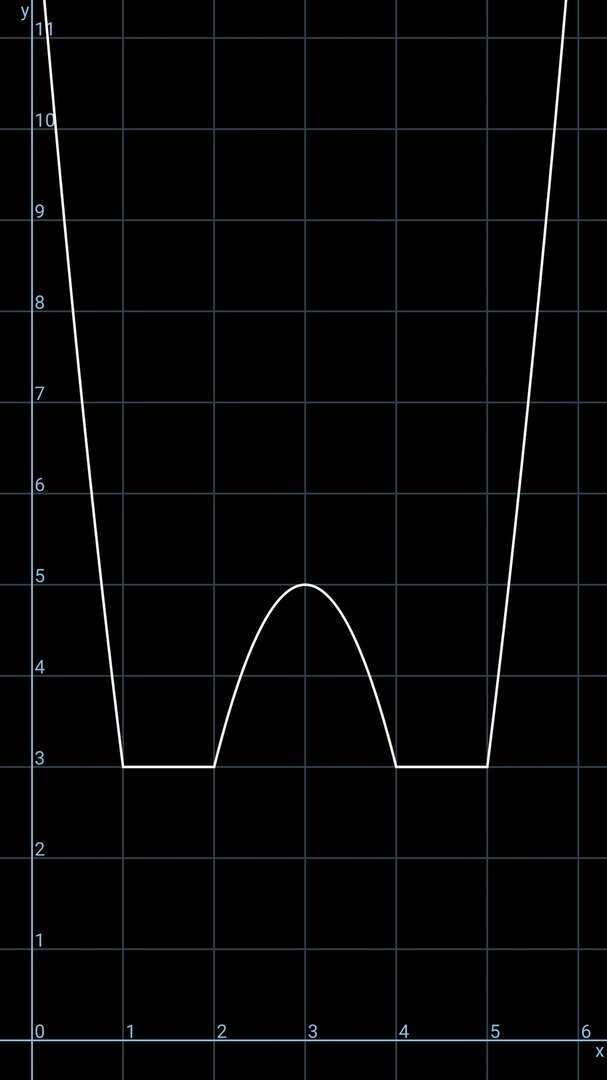
Её график представлен на рис. 2.
у = a - это прямая, параллельная оси Ox. Количество решений уравнения - количество пересечений двух графиков. По рисунку видно, что:
1) нет решений при a < 3
2) 2 решения при a > 5
3) 3 решения при a = 5
4) 4 решения при 3 < a < 5
5) бесконечно много решений при a = 3
215. Построим график функции . Заметим, что функция чётная. Тогда построим график для неотрицательных x и отразим по Oy. Тогда функция для x ≥ 0 примет вид:
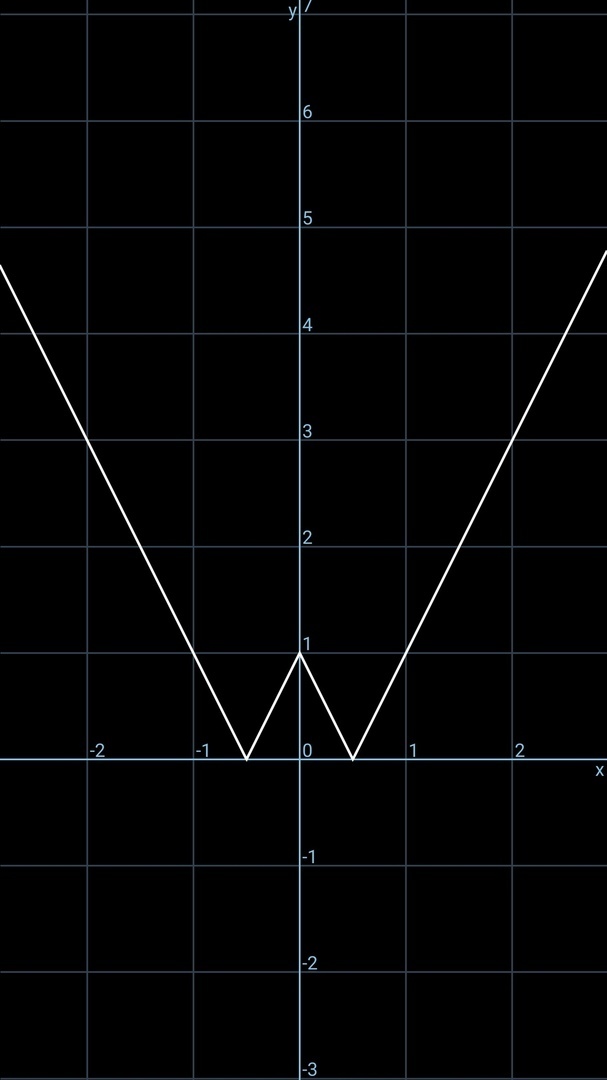
График всей функции представлен на рис. 3.
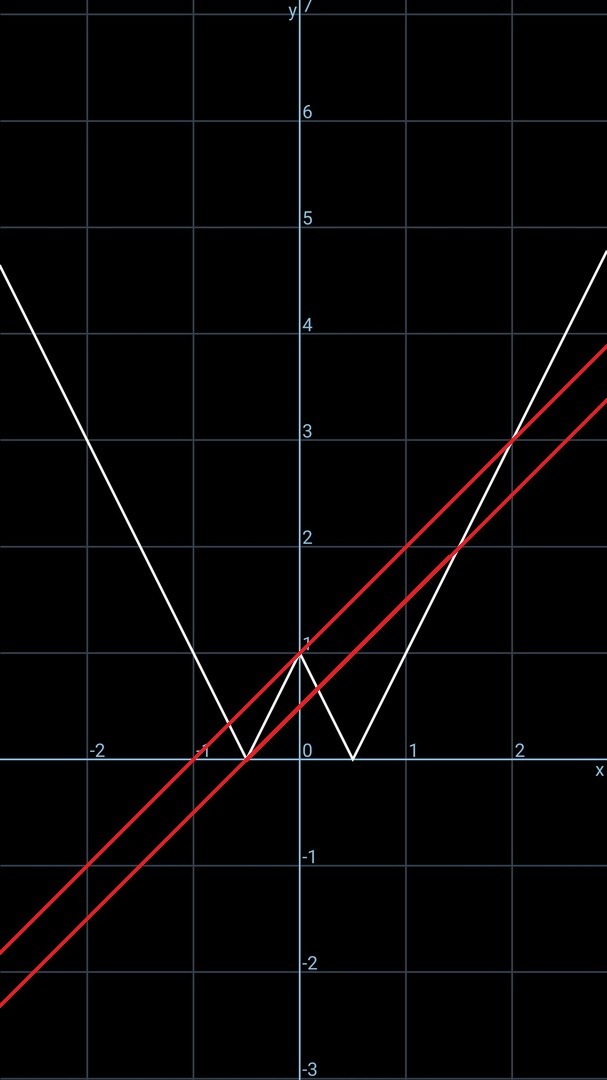
Функция y = x - a - это прямая с коэффициентом наклона прямой k = 1, которая перемещается вверх-вниз. На рис. 4 показаны все случаи, когда прямая имеет с графиком 3 пересечения: когда проходит через точку (-0,5; 0) и через (0; 1). Подставим их координаты в уравнение y = x - a.
1) 0 = -0,5 - a ⇔ a = -0,5
2) 1 = 0 - a ⇔ a = -1
Ответ: -1; -0,5