исследуйте функцию с помощью производной и постройте ее график f(x)=2+x^2-1/3×x^3
Ответы
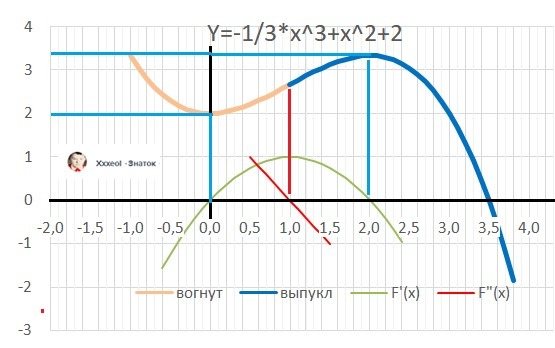
ДАНО: Y= - 1/3*x³ + x² + 2
ИССЛЕДОВАТЬ.
1.Область определения D(x) - Х∈(-∞;+∞) - непрерывная.
2. Пересечение с осью Х. Y=0 при х1 ≈ 3.45. (один)
Положительна - X∈(-∞;x1), отрицательна - X∈(x1;+∞).
3. Пересечение с осью У. У(0) = 2.
4. Поведение на бесконечности. limY(-∞) = + ∞. limY(+∞) = -∞
5. Исследование на чётность. Y(-x) = 1/3*x³+ x²+2 ≠ - Y(x).
Функция ни четная, ни нечётная.
6. Производная функции. Y'(x)= -x² +2*х = -x*(x-2).
Корни при x1 = 0 и х2 = 2. Схема знаков производной.
(-∞)__(>0)__(0)___(<0)___(2)__(>0)_____(+∞)
7. Локальные экстремумы.
Максимум Ymax(2)= 3 1/3, минимум – Ymin(0)= -2.
8. Интервалы монотонности.
Возрастает - Х∈[0;2], убывает = Х∈(-∞;0]∪[2;+∞).
8. Вторая производная - Y"(x) = -2*x + 2 = -2*(x - 1)=0.
Корень производной - точка перегиба x = 1.
9. Выпуклая “горка» Х∈(1;+∞), Вогнутая – «ложка» Х∈(-∞;1).
10. График в приложении.