Предмет: Алгебра,
автор: esmira06
решите иррациональное неравенство
Приложения:
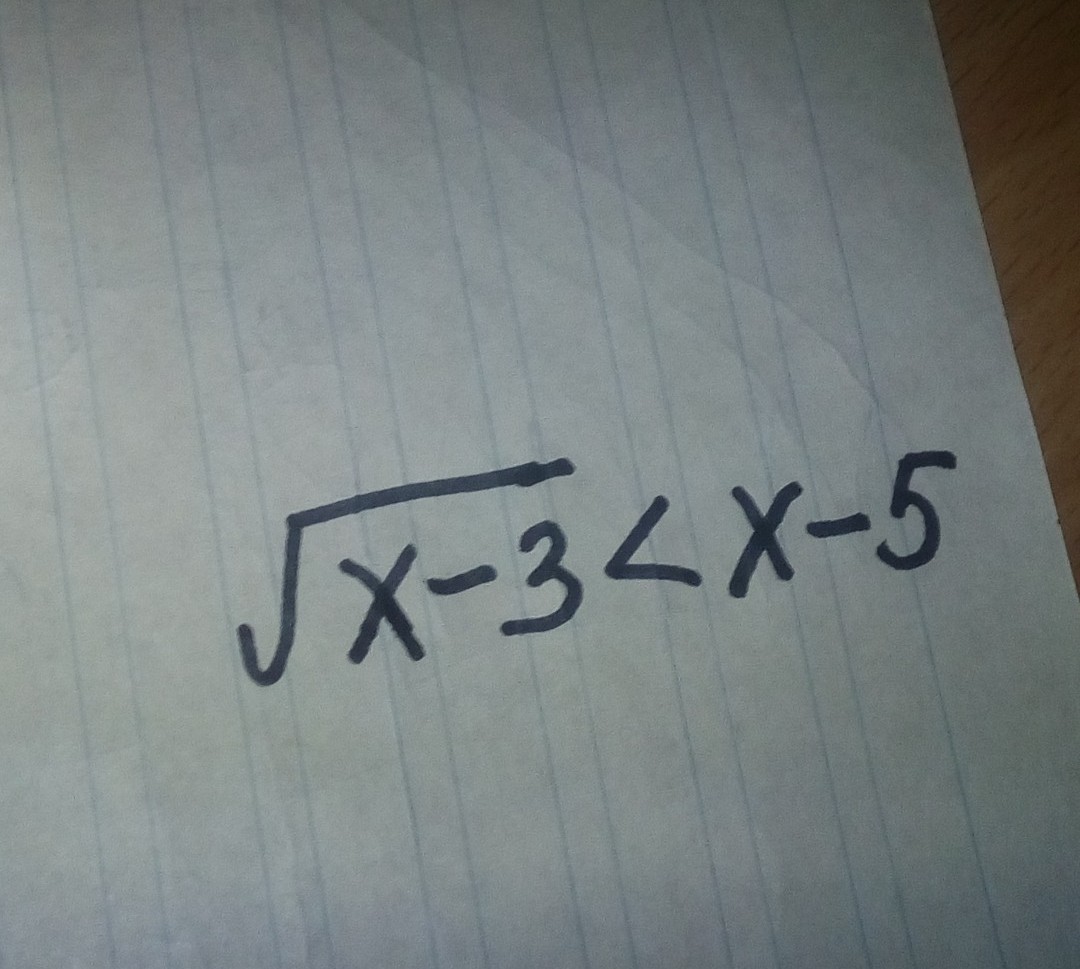
Ответы
Автор ответа:
1
1.
2.
и
=======================
Похожие вопросы
Предмет: Алгебра,
автор: alexmerkulov222
Предмет: Литература,
автор: dimabalcev9
Предмет: Биология,
автор: tugovshurik
Предмет: Химия,
автор: altinbek2017
Предмет: Алгебра,
автор: karkusha2000