Question

Доведіть ,що середини сторін квадрата є вершинами іншого квадрата

Answer 1

Докажите, что середины сторон квадрата являются вершинами другого квадрата.

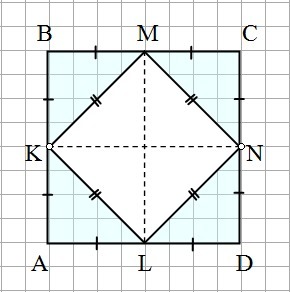
1). Рассмотрим треугольники в углах исходного квадрата, - KBM; MCN; NDL; LAK. Все они являются равнобедренными прямоугольными треугольниками с равными катетами.

Следовательно, их гипотенузы также равны: KM = MN = NL = LK.

Кроме того, так как углы при гипотенузах равны 45°, то:

∠KMN = ∠MNL = ∠NLK = ∠LKM = 90°

Получили:

     KMNL - ромб с углами по 90° =>  KMNL является квадратом.

2). Проведем в четырехугольнике KMNL диагонали ML и KN.

Так как BK = CN = AK = ND, то ВС || KN || AD

Аналогично: AB || ML || CD.

Следовательно: ML⊥KN, причем: ML = KN.

Значит KMNL - ромб с равными диагоналями, т.е. KMNL - квадрат.