Предмет: Алгебра,
автор: alell66
Найти максимум функции y=x^2-34x+144lnx+6
Ответы
Автор ответа:
1
Найдём производную функции:
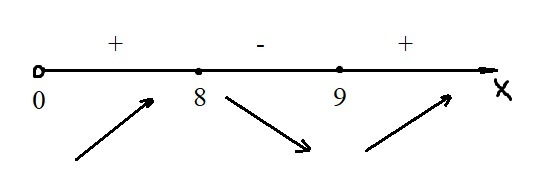
Посмотрим, как ведёт себя функция (см. рис.). Видно, что возрастание сменяется убыванием в точке x = 8. Значение в точке максимума:
Ответ:
Приложения:
Похожие вопросы
Предмет: Математика,
автор: irinamomot325
Предмет: Русский язык,
автор: ler1451
Предмет: Русский язык,
автор: amirtatykhojayev
Предмет: Математика,
автор: SkipperMen
Предмет: Математика,
автор: SkipperMen