Question

2 и 4, пожалуйстааааааааааааа

Answer 1

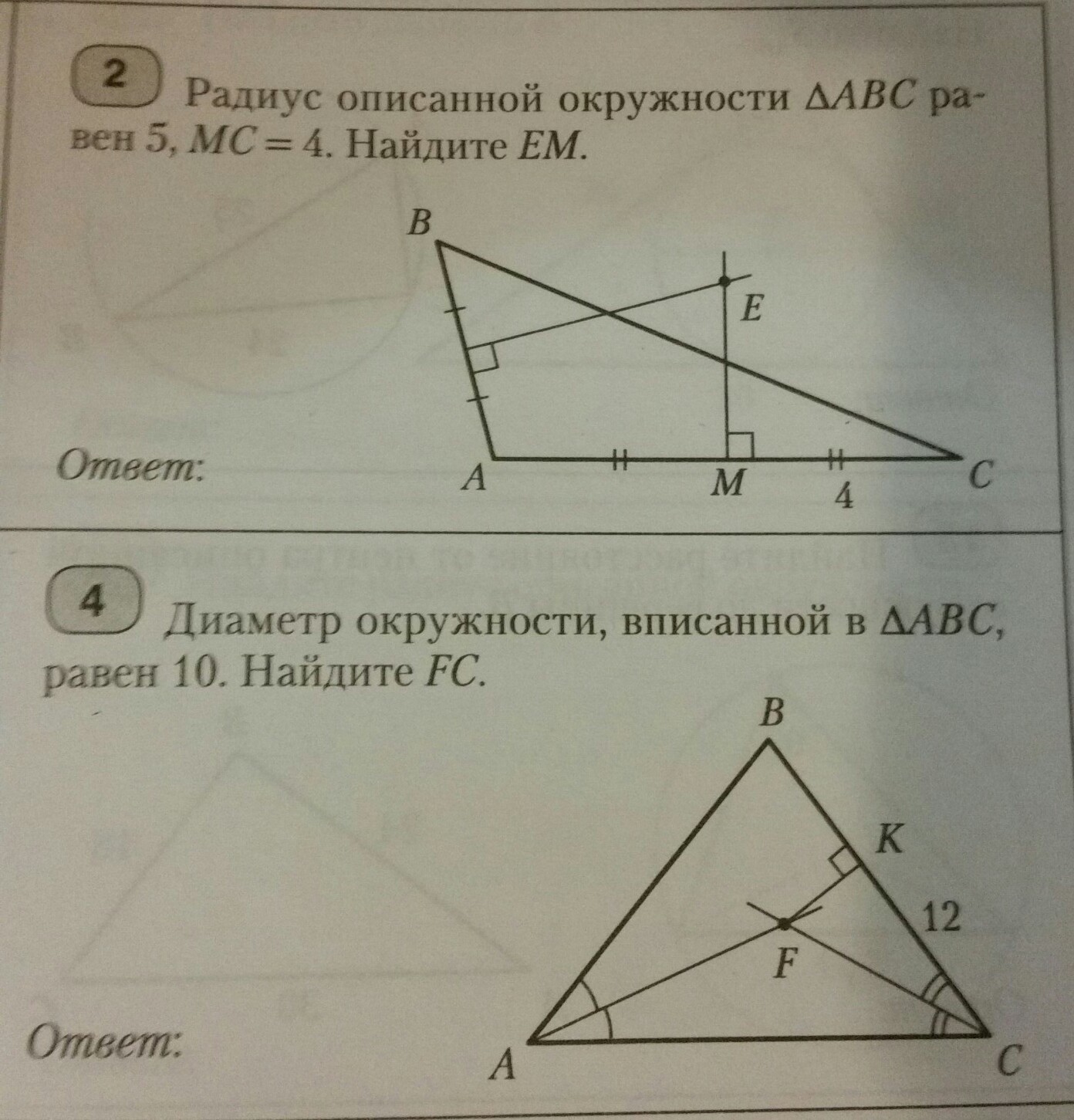
2) Центром описанной окружности около треугольника является точка пересечения серединных перпендикуляров. Центр описанной окружности равноудалён от вершин данного треугольника. Следовательно, АЕ = ВЕ = СЕ = 5 - радиус описанной окружности.
Рассмотрим тр. ЕМС: по т. Пифагора
ЕМ = V( 5^2 - 4^2 ) = V( 25 - 16 ) = V9 = 3

ОТВЕТ: 3

3) Центром вписанной окружности в треугольник является точка пересечения биссектрис. Центр вписанной окружности равноудалён от сторон данного треугольника. Следовательно, FK = 10/2 = 5 - радиус вписанной окружности.
Рассмотрим тр. FKC: по т. Пифагора
FC = V( 5^2 + 12^2 ) = V( 25 + 144 ) = V169 = 13

ОТВЕТ: 13.