Предмет: Алгебра,
автор: ЯПромолчу
Помогите! Решить по правилу Лопиталя.
Приложения:
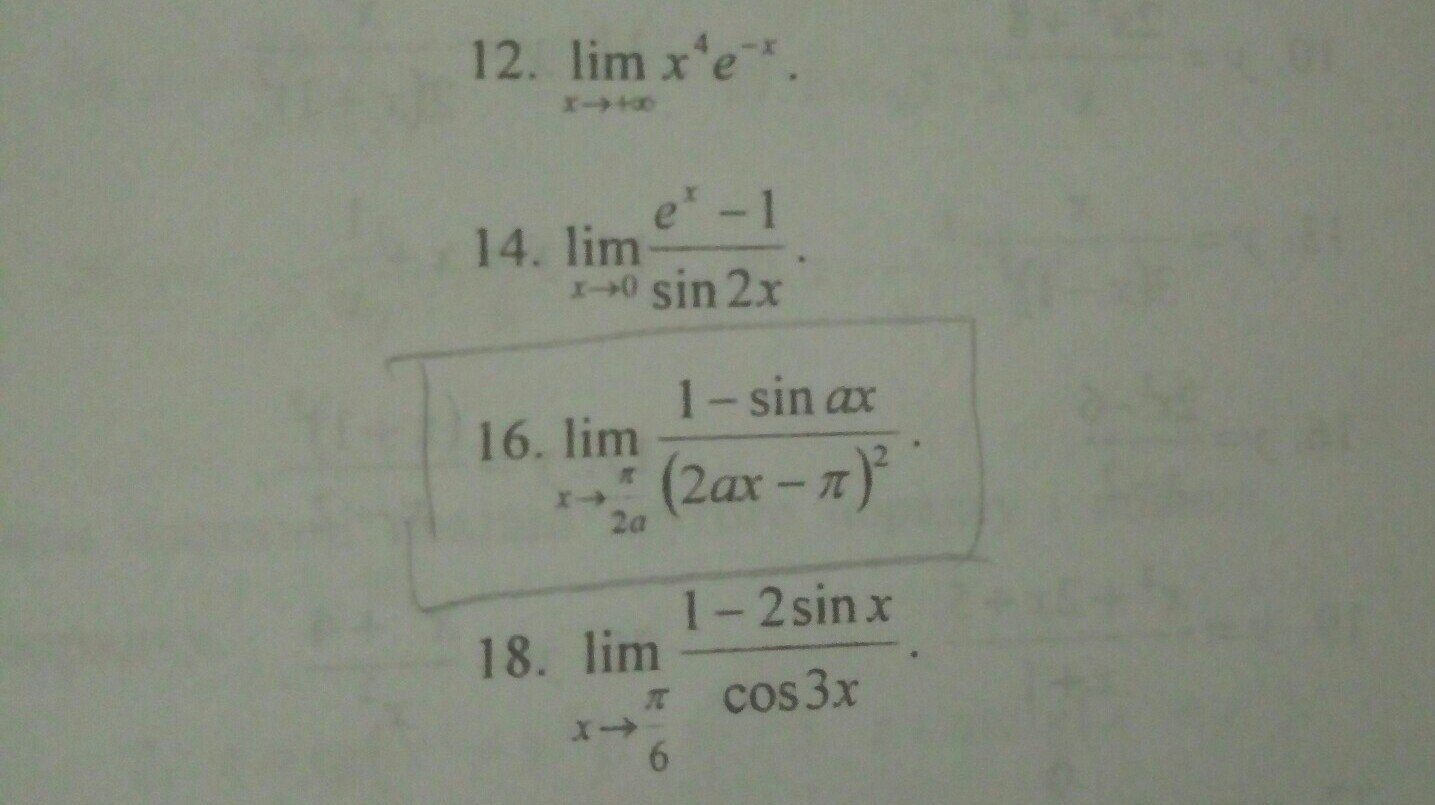
Ответы
Автор ответа:
3
Берём производные от числителя и знаменателя, считая a константой.
ЯПромолчу:
Огромное спасибо)
Похожие вопросы
Предмет: Русский язык,
автор: tanyaborovskaya48525
Предмет: Физика,
автор: Vektor200907
Предмет: Математика,
автор: yanasralavshtani
Предмет: Математика,
автор: рая42
Предмет: Математика,
автор: SonyaMironova