Предмет: Алгебра,
автор: polishka1910
Помогите пожалуйста решить ряд
Приложения:
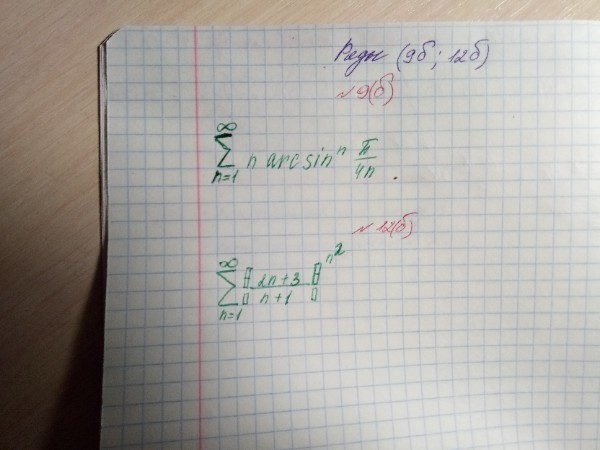
Ответы
Автор ответа:
1
Если требуется исследовать ряды на сходимость, то можно в обоих случаях использовать радикальный признак Коши.
1)
Здесь встретился довольно редко использующийся в учебных заданиях предел . В курсе анализа доказывается, что этот предел равен 1.
Тогда
Предел меньше 1, поэтому ряд сходится.
2)
Ряд расходится.
Похожие вопросы
Предмет: Физика,
автор: alina28336
Предмет: Математика,
автор: Аноним
Предмет: Литература,
автор: ariaskapahluk
Предмет: Алгебра,
автор: crazy145
Предмет: Математика,
автор: настя488к