Предмет: Алгебра,
автор: AnnaSergeevna87
найти производную функции при заданном значении аргумента
Приложения:
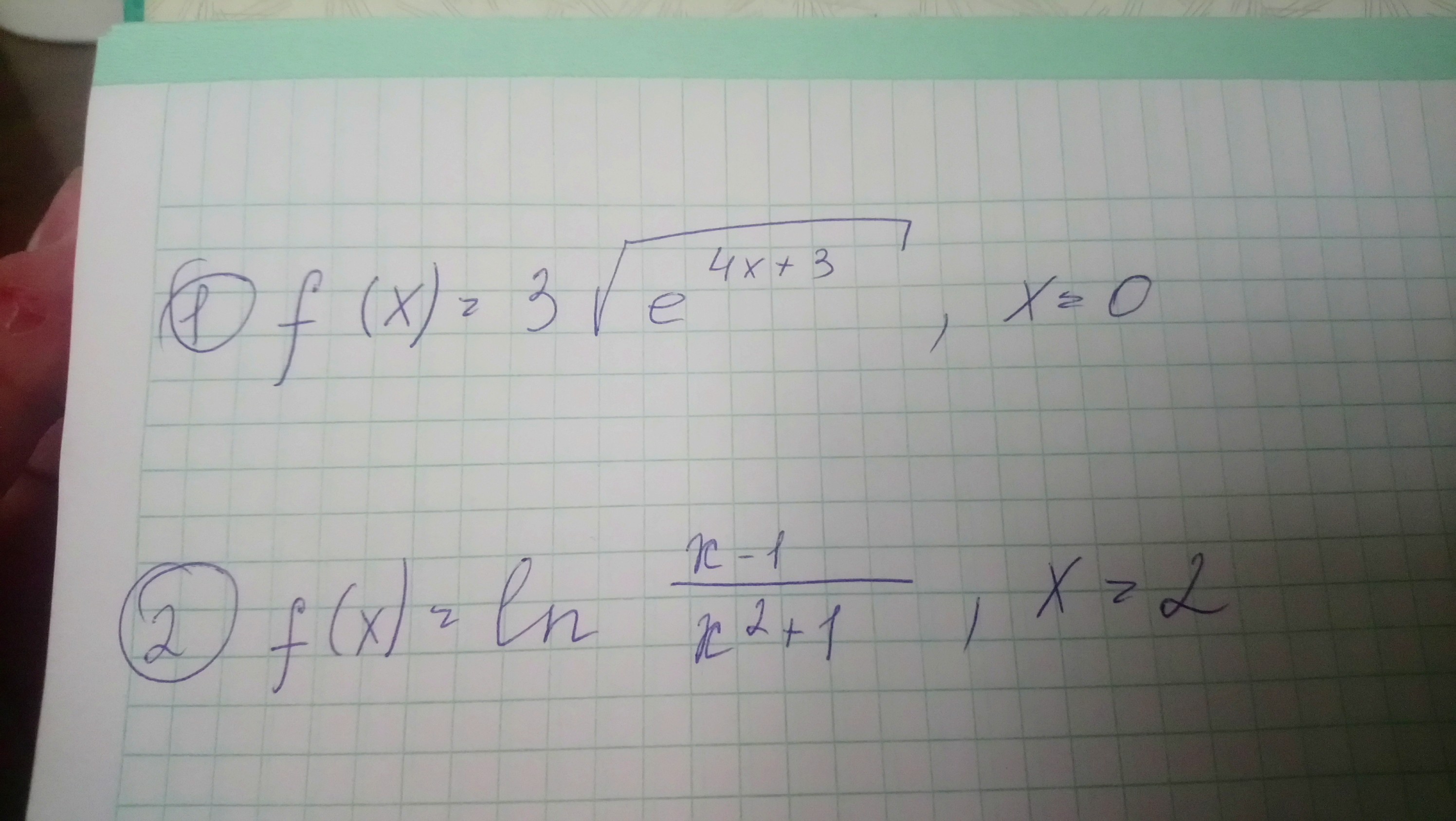
Ответы
Автор ответа:
5
Похожие вопросы
Предмет: Информатика,
автор: dekkek1234
Предмет: Физика,
автор: mistyusha595
Предмет: Геометрия,
автор: abujnova0
Предмет: Математика,
автор: Vtr123
Предмет: Математика,
автор: xdxhtgcfr