Решите неравенство, пожалуйста.
Ответ: при а=0 не имеет смысла. При а=3 х€R. При а не=0 и при а не=3 х=3а
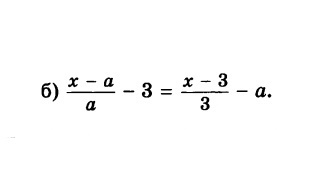
Ответы
Такие уравнения называются уравнениями с параметром.
решая их - нужно учитывать все возможные случаи изменения параметра.
1) у нас два дроби. В первой дроби в знаменателе стоит параметр "а" .
и по свойствам дроби "а" не может равнятся 0
Значит если вдруг наш параметр примет значение 0,
то данное уравнение просто потеряет смысл. Т.е. решений не будет.
2) теперь решим наше уравнение при условии что "а"≠0
Теперь смотрим что получилось
если а=3 то
(3-3)*(x-9)=0
т.е. выражение равно нулю при любом х
и еще один случай, когда а≠3
И мы получили такое решение:
-при а=0 решений нет
- при а=3 Равентсво выполняется для любого х
- при а≠3 и а≠0 Х=3а
task/30445166 Решить УРАВНЕНИЕ (x -a)/a -3 = (x-3)/3 - a
решение (x -a)/a - 3 = (x-3)/3 - a. ОДЗ : a ≠ 0
x -a)/a - 3 =(x-3)/3 - a ⇔ x/a - 1 - 3= x/3 -1 - a ⇔ x/a -x/3 = 3 - a ⇔
( (3-a)/3a ) *x = 3 - a . * * * A*x = B * * *
если 3 -a = 0 , т.е. a=3 получается 0*x =0 , x любое число x ∈ R
если a ≠3 и a ≠ 0→ (ОДЗ) , то x = (3-a) : (3-a)/3a = 3a