Предмет: Алгебра,
автор: nastya1803031
60 баллов
Помогите, пожалуйста, решить номер 2(б) - ответ х€R и номер 3 - ответ (-4;4)
Приложения:
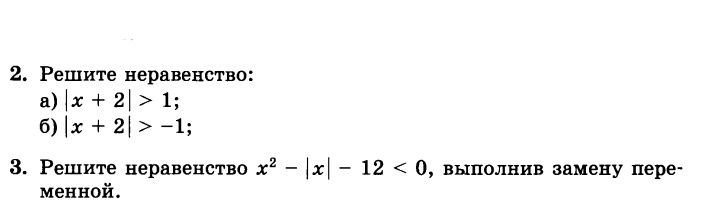
MizoriesKun:
сейчас будет супер ответ , модератор пишет
Ответы
Автор ответа:
1
task/30442737
2б) | x+2| > - 1 ОДЗ : x ∈ ( -∞ ; + ∞)
по определению | x+2| ≥ 0 ⇒ | x+2| > - 1 при всех x . x ∈ R
3) x² - |x| - 12 < 0 ⇔ |x|² - |x| - 12 < 0 . замена: t = |x| ≥ 0
t² - t - 12 < 0 ⇔ (t + 3)(t - 4) < 0 ⇔ - 3 < t < 4
+ + + + + + + ( -3) //////////////// (4) + + + + + + +
Обратная замена: - 3 < |x| < 4 ⇔ |x| < 4 ⇔ - 4 < x < 4 || x ∈ (- 4 ; 4 ) ||
* * * |x| > - 3 для всех x ; x ∈ ( -∞ ; + ∞) * * *
ответ: x ∈ (- 4 ; 4 ) .
t² - t - 12 =0 D =1²- 4*1*(-12) =1+48=49 =7² ; t₁,₂ =(1 ±7)/2⇒ t₁= -3 , t₂= 4
* * * t² - t - 12 =t² + 3t -4t - 12=t(t +3) - 4(t +3) = (t +3)(t -4) * * *
* * |x|²- |x| - 12 < 0 ⇔( |x| +3)(|x| - 4) < 0⇔ |x| - 4 < 0, т.к. |x| +3 >0 * * *
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Английский язык,
автор: lama333
Предмет: Алгебра,
автор: vidriknadia249
Предмет: Алгебра,
автор: alima22