Предмет: Алгебра,
автор: zrfnzk
Срочно. Помогите пожалуйста. Много баллов. № 73(5;6) Найти производную функции.
Приложения:
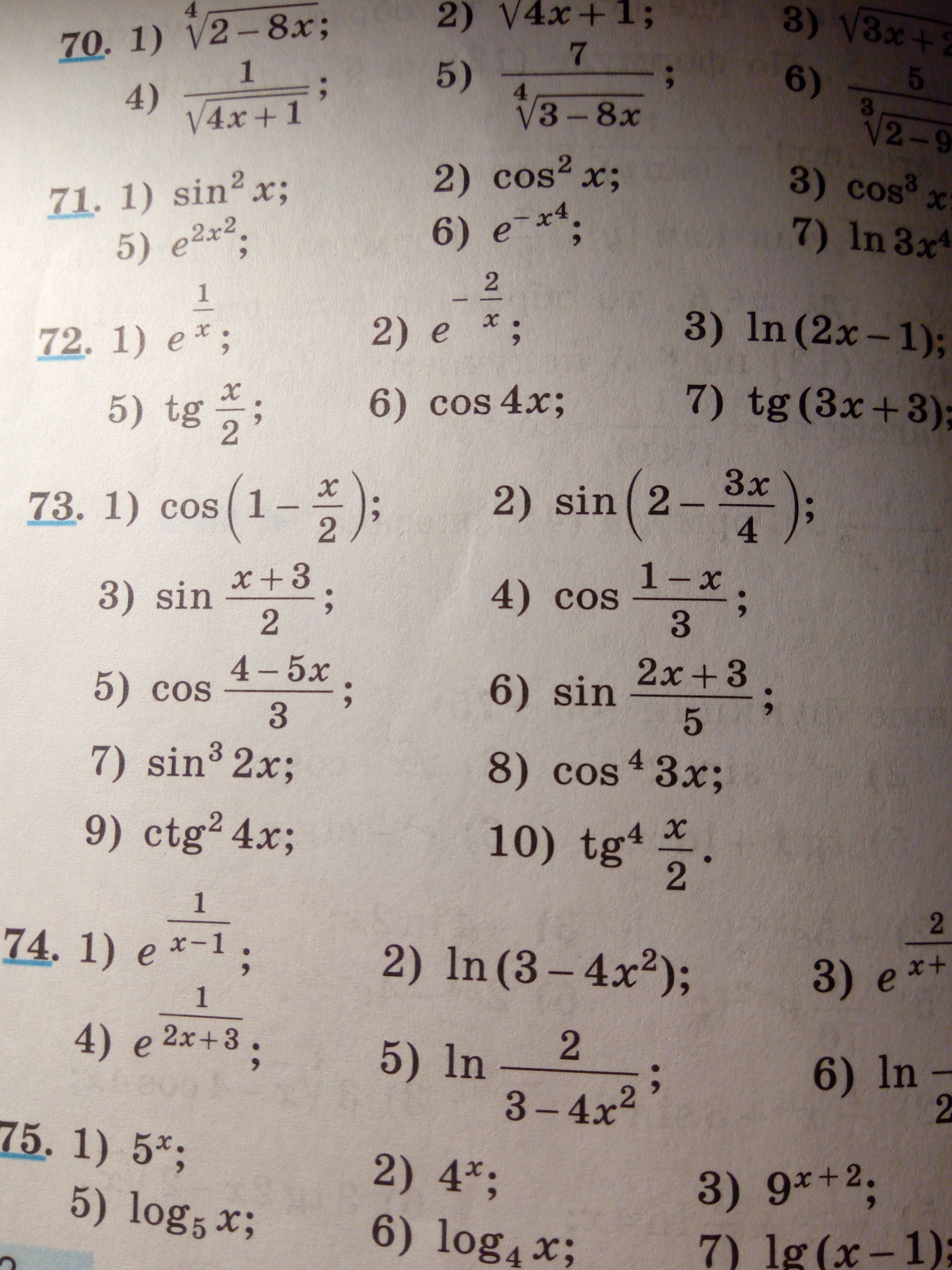
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Обществознание,
автор: milkowf
Предмет: Математика,
автор: engilili2206
Предмет: Английский язык,
автор: Geh28b3veuwu
Предмет: Алгебра,
автор: Alim23