Предмет: Геометрия,
автор: Novaya22
100 баллов!
Основанием пирамиды есть треугольник со сторонами 13, 20, 21см. Если двогранные углы при основании =30° каждый, то чему равен обьем пирамиды? Решение обязательно с рисунком.
Ответы
Автор ответа:
2
Основанием пирамиды есть треугольник со сторонами 13, 20, 21 см. Если двугранные углы при основании равны 30° каждый, то чему равен обьем пирамиды?
РЕШЕНИЕ:
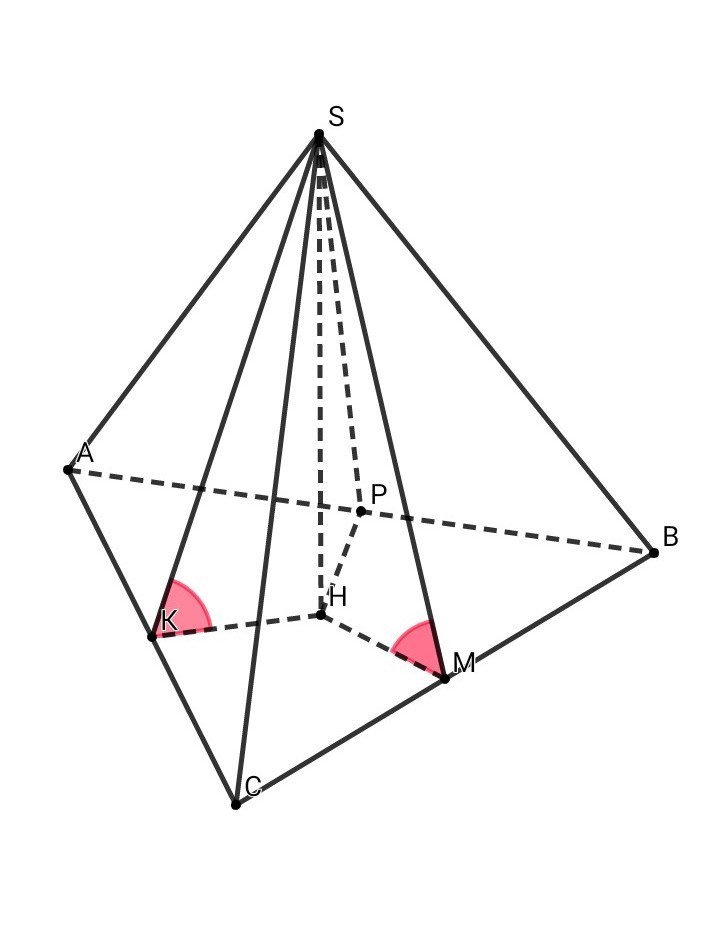
• Из точки Н, основания перпендикуляра SH , проведём перпендикуляр к ВС в точке М .
• SH перпендикулярен НМ, НМ перпедикулярен ВС => по теореме о трёх перпендикулярах SM перпендикулярен ВС.
Аналогично, проводя перпендикуляры из точки Н к сторонам треугольника АВС получаем: SK перпедикулярен АС , SP перпедикулярен AB
• тр. SKH = тр. SMH = тр. SPH по катету и прилежащему углу ( SH - общий катет , угол KSH = угол МSH = угол PSH = 60° )
Значит, HK = HM = HP, но при этом НК перпедикулярен АС , НМ перпедикулярен ВС, НР перпедикулярен АВ => Значит, HK = HM = HP = r - радиусы вписанной окружности в тр. АВС.
• Найдём площадь тр. АВС по формуле Герона:

где р = ( a + b + c ) / 2 - полупериметр , a, b, c - стороны данного треугольника

• Используем формулу для нахождения радиуса вписанной окружности:

HK = HM = HP = r = 14/3 см
• Рассмотрим тр. SHM (угол SHM = 90°):
tg30° = SH / HM => SH = tg30° • ( 14 / 3 ) = ( V3 / 3 ) • ( 14 / 3 ) = 14V3 / 9 см
• V пир. = ( 1/3 ) • S abc • SH = ( 1/3 ) • 126 • ( 14V3 / 9 ) = ( 126/27 ) • 14V3 = ( 14/3 ) • 14V3 = 196V3 / 3 см^3
ОТВЕТ: 196V3 / 3 см^3
РЕШЕНИЕ:
• Из точки Н, основания перпендикуляра SH , проведём перпендикуляр к ВС в точке М .
• SH перпендикулярен НМ, НМ перпедикулярен ВС => по теореме о трёх перпендикулярах SM перпендикулярен ВС.
Аналогично, проводя перпендикуляры из точки Н к сторонам треугольника АВС получаем: SK перпедикулярен АС , SP перпедикулярен AB
• тр. SKH = тр. SMH = тр. SPH по катету и прилежащему углу ( SH - общий катет , угол KSH = угол МSH = угол PSH = 60° )
Значит, HK = HM = HP, но при этом НК перпедикулярен АС , НМ перпедикулярен ВС, НР перпедикулярен АВ => Значит, HK = HM = HP = r - радиусы вписанной окружности в тр. АВС.
• Найдём площадь тр. АВС по формуле Герона:
где р = ( a + b + c ) / 2 - полупериметр , a, b, c - стороны данного треугольника
• Используем формулу для нахождения радиуса вписанной окружности:
HK = HM = HP = r = 14/3 см
• Рассмотрим тр. SHM (угол SHM = 90°):
tg30° = SH / HM => SH = tg30° • ( 14 / 3 ) = ( V3 / 3 ) • ( 14 / 3 ) = 14V3 / 9 см
• V пир. = ( 1/3 ) • S abc • SH = ( 1/3 ) • 126 • ( 14V3 / 9 ) = ( 126/27 ) • 14V3 = ( 14/3 ) • 14V3 = 196V3 / 3 см^3
ОТВЕТ: 196V3 / 3 см^3
Приложения:
Novaya22:
А остальные задачи не сможете сделать?
К сожалению, сил уже нет. Попросил товарища, он поможет Вам)
Похожие вопросы
Предмет: Литература,
автор: timursmirnovv875
Предмет: История,
автор: Аноним
Предмет: Алгебра,
автор: zhasmin242008
Предмет: Литература,
автор: advays2016
Предмет: История,
автор: Никитаизи