Предмет: Алгебра,
автор: Trolshik
СРОЧНО! ПОМОГИТЕ С ЭТИМИ ЗАДАНИЯМИ ПОЖАЛУЙСТА
Приложения:
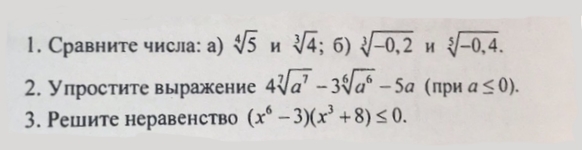
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: glebschapik
Предмет: Английский язык,
автор: Аноним
Предмет: Химия,
автор: fdsxgkyhvv
Предмет: Литература,
автор: ОстерА
Предмет: Математика,
автор: irinkayakovenko