Предмет: Геометрия,
автор: mnogotochie
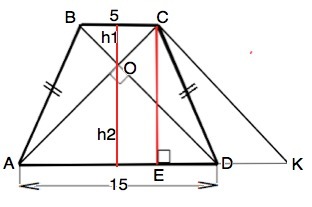
АВСD-трапеция. AD=15 см, BC=5. диагонали AC и BD,EC-высота, угол CED-прямой, угол на пересечении диагоналей равен 90градусов. Найти СЕ
Ответы
Автор ответа:
0
Условие дано не полностью. Это одна из задач по готовым рисункам.
Правильно: АВСD- равнобедренная трапеция. AD=15 см, BC=5. диагонали AC и BD пересекаются в точке О под прямым углом. Найти высоту ЕС.
-------------------------------------
Вариант решения 1)
Проведем через вершину С параллельно АВ прямую до пересечения с продолжением АD в точке К.
Четырехугольник ВСКD - параллелограмм ( ВС║АК по условию, СК║ВD по построению). Следовательно, DК=ВС=5.
В равнобедренной трапеции диагонали равны.
Так как СК║ВD, то ∠АСК =∠АОD как соответственные при пересечении параллельных прямых секущей.
Следовательно, треугольник АСК прямоугольный равнобедренный, его высота, как высота равнобедренного треугольника, является его медианой,
Медиана прямоугольного треугольника равна половине гипотенузы.
Значит, СЕ=АЕ=ЕК.
АD+DK=15+5=20
CE=20:2=10 см
* * *
Вариант решения 2)
В равнобедренной трапеции диагонали равны и при пересечении образуют подобные треугольники, основания которых - основания трапеции.
Треугольник ВОС - равнобедренный прямоугольный, его высота является медианой и по свойству медианы прямоугольного треугольника равна половине основания.
h₁ ∆ ВОС=2,5 см
Аналогично высота ∆ АОD h₂=15:2=7,5 см
Высота трапеции равна сумме высот треугольников ВОС и АОD и равна СЕ.
СЕ=h₁+h₂=2,5+7,5=10 см.
Правильно: АВСD- равнобедренная трапеция. AD=15 см, BC=5. диагонали AC и BD пересекаются в точке О под прямым углом. Найти высоту ЕС.
-------------------------------------
Вариант решения 1)
Проведем через вершину С параллельно АВ прямую до пересечения с продолжением АD в точке К.
Четырехугольник ВСКD - параллелограмм ( ВС║АК по условию, СК║ВD по построению). Следовательно, DК=ВС=5.
В равнобедренной трапеции диагонали равны.
Так как СК║ВD, то ∠АСК =∠АОD как соответственные при пересечении параллельных прямых секущей.
Следовательно, треугольник АСК прямоугольный равнобедренный, его высота, как высота равнобедренного треугольника, является его медианой,
Медиана прямоугольного треугольника равна половине гипотенузы.
Значит, СЕ=АЕ=ЕК.
АD+DK=15+5=20
CE=20:2=10 см
* * *
Вариант решения 2)
В равнобедренной трапеции диагонали равны и при пересечении образуют подобные треугольники, основания которых - основания трапеции.
Треугольник ВОС - равнобедренный прямоугольный, его высота является медианой и по свойству медианы прямоугольного треугольника равна половине основания.
h₁ ∆ ВОС=2,5 см
Аналогично высота ∆ АОD h₂=15:2=7,5 см
Высота трапеции равна сумме высот треугольников ВОС и АОD и равна СЕ.
СЕ=h₁+h₂=2,5+7,5=10 см.
Приложения:
Похожие вопросы
Предмет: Биология,
автор: 666sq777qq
Предмет: Математика,
автор: kykudaniil
Предмет: Қазақ тiлi,
автор: uu749811
Предмет: Математика,
автор: 30112
Предмет: Математика,
автор: клеопатра45