Предмет: Математика,
автор: SergeyOrlov001
Найти экстремумы функции
1/4(x-3)^2(x+3)
Подробно молю, пожалуйста.
Вся сложность в взятии производной..
Приложения:
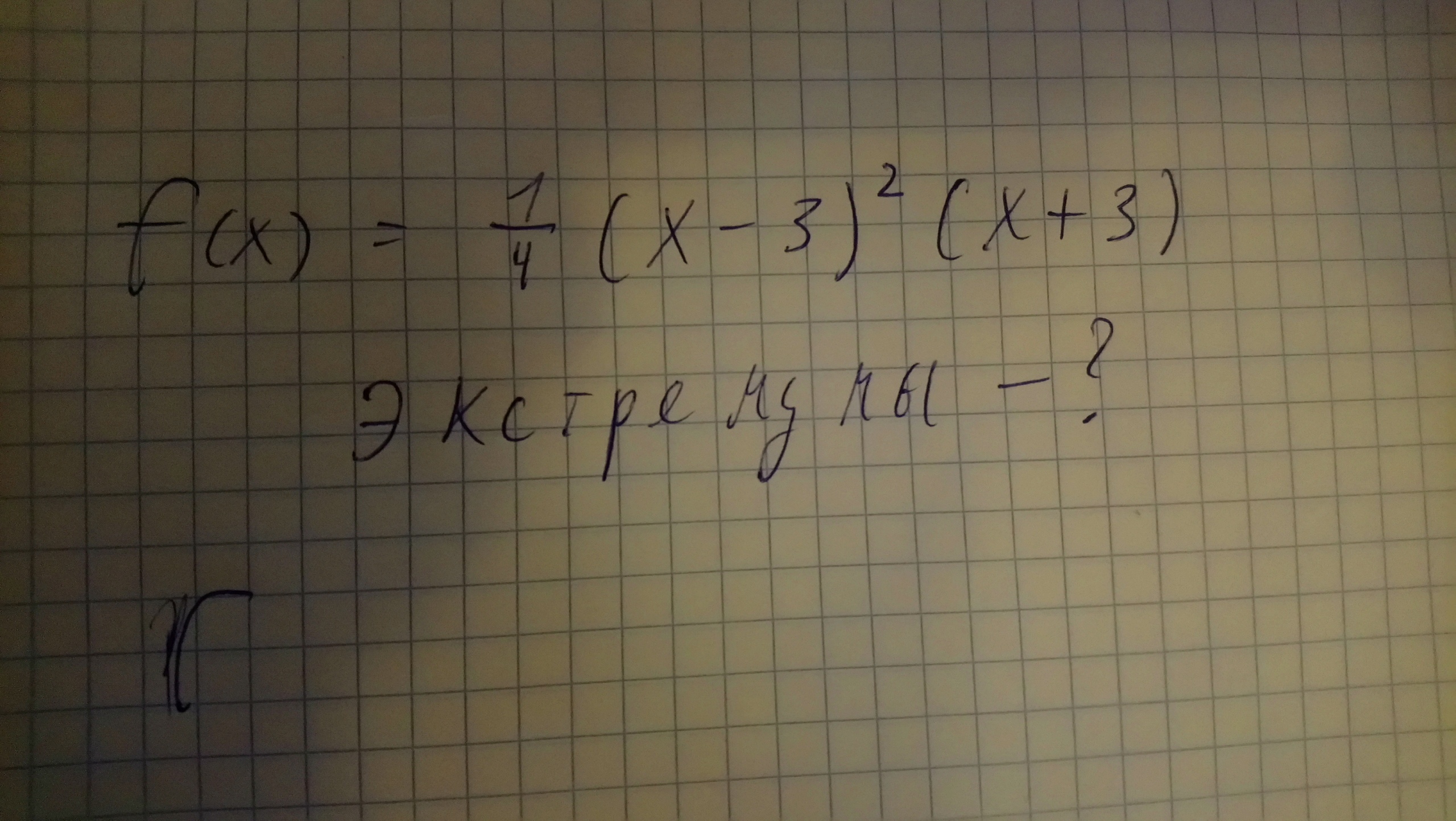
Ответы
Автор ответа:
1
Точка называется экстремумом функции если производная функции в этой точке равна нулю.
Проверяем, какая из точек является минимумом функции f(x), а какая максимумом.
Если при переходе через точку x1 производная функции меняет знак с плюса на минус, то х1 - точка масимума функции, если с минуса на плюс, то х1 - точка минимума функции.
-знак +
- знак минус
- знак плюс
Таким образом
- максимум функции
- минимум функции
Похожие вопросы
Предмет: Математика,
автор: kolosovdimka333
Предмет: Алгебра,
автор: vila3385
Предмет: Алгебра,
автор: pavel070707abramov
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: singapore7