Question

Докажите,что когда 2 дуги круга равны,то равны и хорды,которые их стягивают.
С решением,рисунком,объяснением,полный,исчерпывающий ответ.

Answer 1

Дано :

Круг, точка О - центр круга.

∪AD = ∪BC.

Доказать :

AD = BC.

Доказательство :

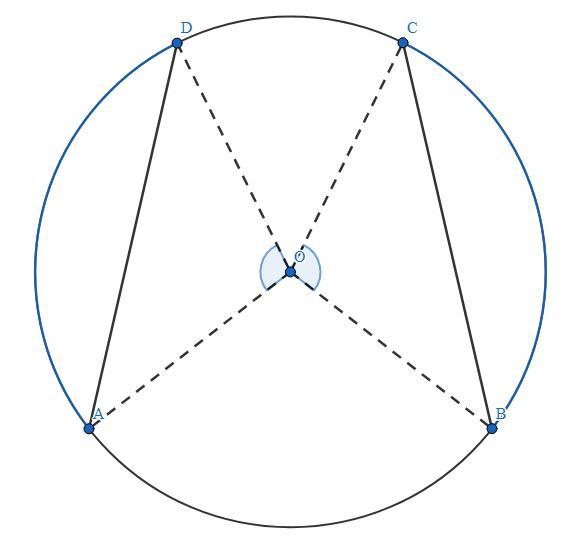
Соединим точки А и О, D и О, В и О, С и О.

Так как ∪AD = ∪BC, то это значит, что и их градусные меры равны.

• Градусная мера центрального угла (угла, вершина которого - центр круга) измеряется градусной мерой дуги, на которую опирается этот угол.

Следовательно, ∪AD = ∠AOD, ∪BC = ∠BOC. И так как по условию ∪AD = ∪BC, то и ∠AOD = ∠BOC.

Рассмотрим ΔAOD и ΔВОС.

АО = DO = CO = BO (так как радиусы одного круга), ∠AOD = ∠BOC (по выше доказанному) ⇒ ΔAOD и ΔВОС по первому признаку равенства треугольников (по двум сторонам и углу между ними).

• В равных треугольниках против равных углов лежат равные стороны.

Так как ∠AOD = ∠BOC, следовательно, AD = BC.

Ответ :

что требовалось доказать.