Предмет: Алгебра,
автор: Natalya16041980
Помогите с 5 заданием
Производная Функции
Приложения:
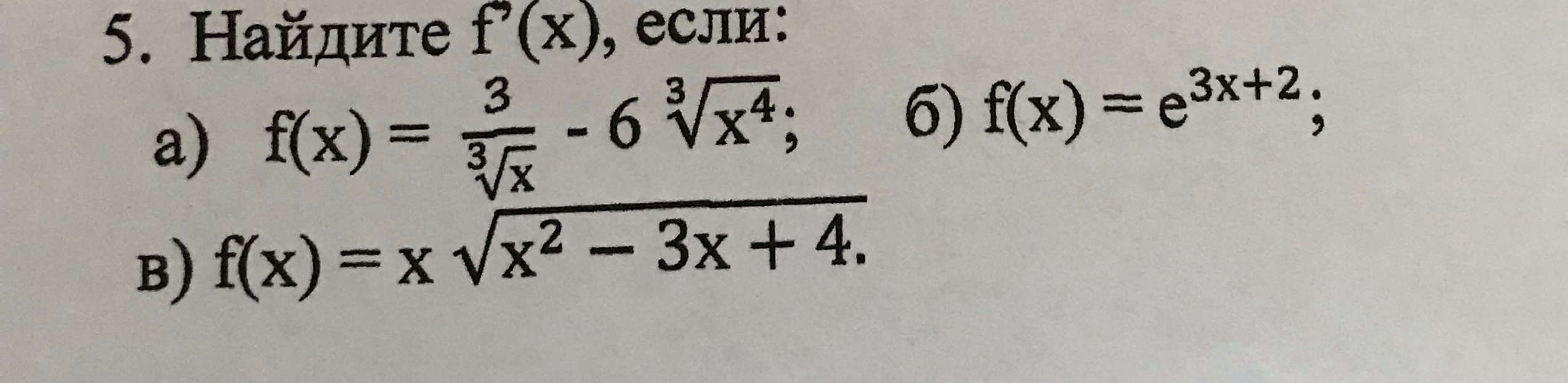
Ответы
Автор ответа:
0
а)
б)
в)
Похожие вопросы
Предмет: Биология,
автор: kirillkiril0988
Предмет: Геометрия,
автор: Dura2836828
Предмет: Математика,
автор: ametovarayhan77
Предмет: Математика,
автор: анна1129
Предмет: Математика,
автор: r3tarded