Предмет: Алгебра,
автор: Аноним
Помогите пожалуйста.
Найти пределы функций, не используя правило Лопиталя
Приложения:
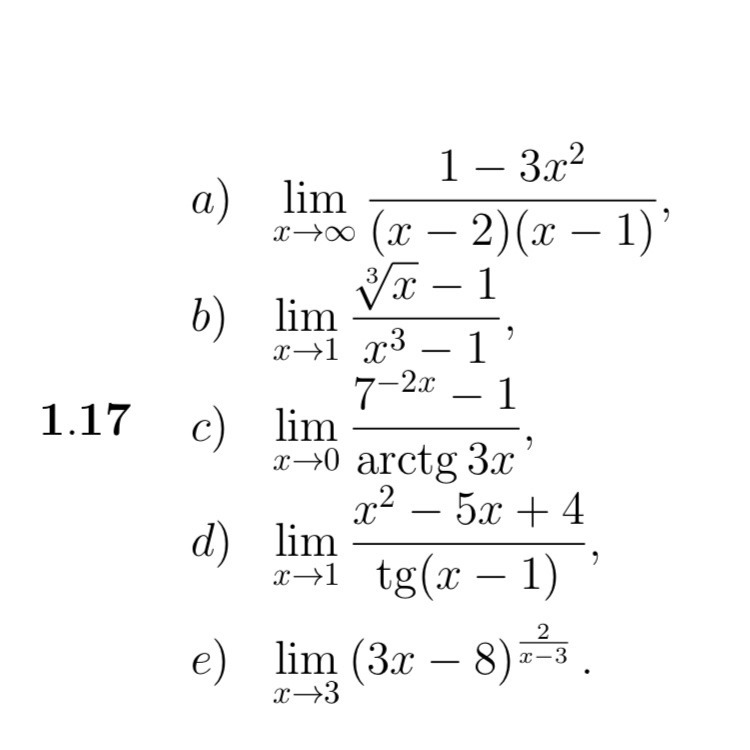
Ответы
Автор ответа:
1
Все переходы - следствия замечательных пределов
a)
b)
c)
d)
e)
Похожие вопросы
Предмет: Алгебра,
автор: e6016138
Предмет: Английский язык,
автор: Аноним
Предмет: Английский язык,
автор: melnicukola2
Предмет: Математика,
автор: nastya060404
Предмет: Математика,
автор: SofiaVaria