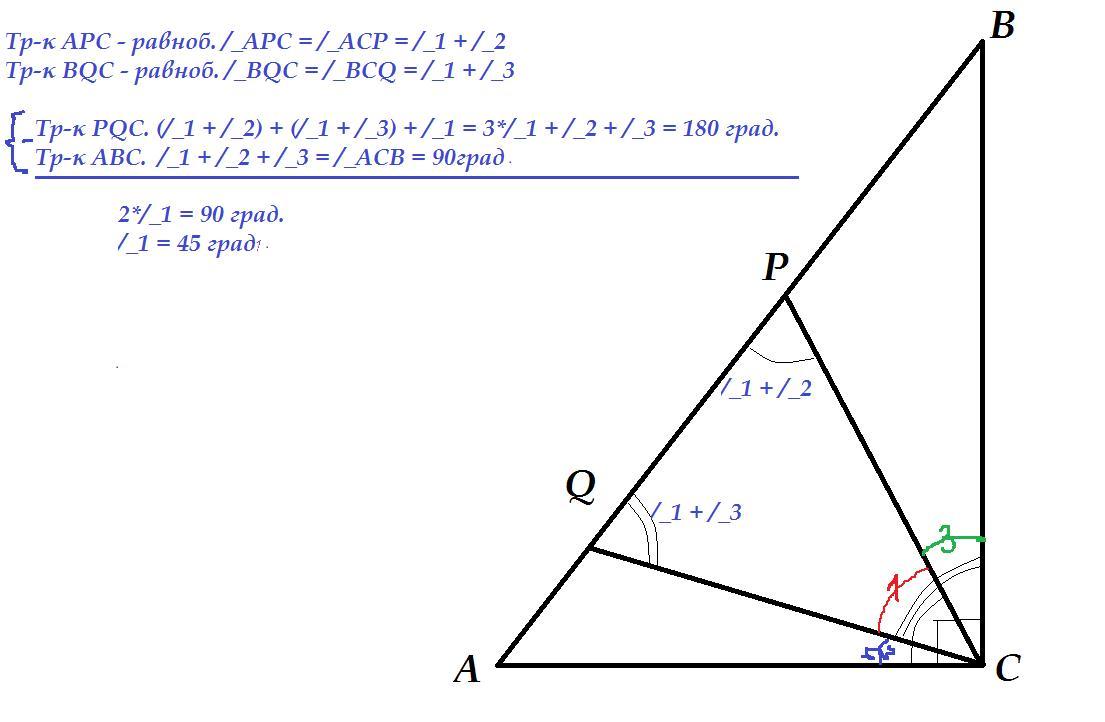
На гипотенузе Ab прямоугольного треугольника Abc выбраны точки P и Q так, что AP=Ac и BQ=BC. Найдите угол PCQ. Ответ дайте в градусах
Ответы
Ответ:
45°
Пошаговое объяснение:
Дано: ΔАВС; ∠АСВ = 90°
АР = АС; ВQ = ВС
Найти: ∠РСQ
Решение.
Рассмотрим Δ АВС. Отрезки СР и CQ делят прямой угол на 3 угла. Для удобства назовем ∠1 искомый ∠PCQ , ∠АСQ, прилежащий к стороне АС, ∠2 и ∠ВСР, прилежащий у стороне ВС ∠3.
∠АСВ = ∠1 + ∠2 + ∠3 = 90° (это уравнение пригодится далее)
Рассмотрим ΔАРС, боковые стороны АР=АС по условию, ⇒ равны углы при основании этого равнобедренного треугольника:
∠АРС = ∠АСР = ∠1 + ∠2.
Рассмотрим ΔВQС, он также равнобедренный по условию (BQ = ВС), ⇒ можно записать равенство углов при его основании:
∠ВQC = ∠BCQ = ∠1 + ∠3
Рассмотрим ΔРQС. Сумма его углов, как и любого треугольника, 180 ° :
∠АРС + ∠ВQC + ∠РСQ = (∠1 + ∠2) + (∠1 + ∠3) + ∠1 = 3 *∠1 + ∠2 + ∠3 = 180°
Имеем систему уравнений, которую можно решить способом вычитания.
{ 3 *∠1 + ∠2 + ∠3 = 180°
{ ∠1 + ∠2 + ∠3 = 90°
2 * ∠1 = 90°
∠1 = 45°
Ответ: 45°