1)докажите что у равнобедренной трапеции углы при основании равны
2)Отрезок соединяющий серидины диагоналей=полуразности оснований трапеции
С РИСУНКАМИ
Ответы
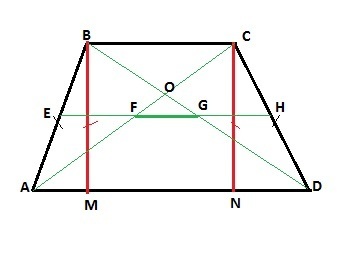
1. Пусть дана РАВНОБОКАЯ трапеция АВСD. Проведем ДВЕ высоты ВM и СN из вершин тупых углов. Образовавшиеся прямоугольные треугольники АВM и DCN равны по катету и гипотенузе. У равных треугольников против равных сторон лежат равные углы. Следовательно, <A = <D, что и требовалось доказать.
2. Соединим середины диагоналей АС и ВD отрезком FG и продлим его в обе стороны до пересечения с боковыми сторонами трапеции АВ и CD в точках Е и H соответственно. В равнобокой трапеции диагонали равны, следовательно, AF=DG и FO=GO (точка О - точка пересечения диагоналей). Тогда в треугольнике АОD отрезок FG параллелен основанию AD. => Прямая ЕН - средняя линия трапеции, а EF и GH - средние линии треугольников АВС и DBC. => EF=GH=BC/2. => EH=BC+FG.
Средняя линия ЕН трапеции равна полусумме ее оснований, то есть ЕН=(BC+AD)/2 => BC+AD=2EH => BC+AD =2(BC+FG). => FG=(AD-BC)/2, что и требовалось доказать.