Question

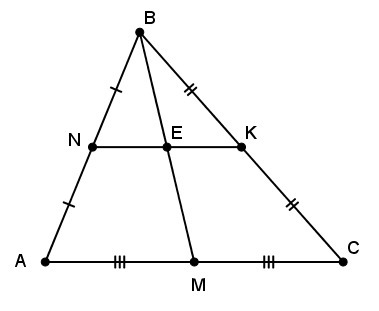
Докажмте , что в треугольнике ABC медиана BM делит среднюю линию NK (N пренадлежит AB, K пренадлежит BC) пополам.

Answer 1

Средняя линия NK параллельна стороне AC и равна её половине:

$NK=\dfrac{1}{2}AC$

Рассмотрим треугольник ABM (см. рисунок). Обозначим точку пересечения NK и медианы BM буквой E. Отрезок NE параллелен стороне AM и проходит через середину стороны AB, а значит, является средней линией:

$NE=\dfrac{AM}{2}=\dfrac{\dfrac{1}{2}AC}{2}=\dfrac{NK}{2}.$

Это и означает, что точка E делит пополам отрезок NK, что и требовалось доказать.

P. S. Медиана, кстати, делит пополам не только среднюю линию, но и любой отрезок, параллельный стороне AC.