Question

100 баллов!
Стороны оснований прямого параллелепипеда =6 и 8см, а угол между ними 60°. Если площадь боковой поверхности параллелепипеда =140, то чему равен его объем ? Решение обязательно с рисунком

Answer 1

Стороны оснований прямого параллелепипеда равны 6 и 8 см, а угол между ними 60°. Если площадь боковой поверхности параллелепипеда равна 140, то чему равен его объем?

РЕШЕНИЕ:

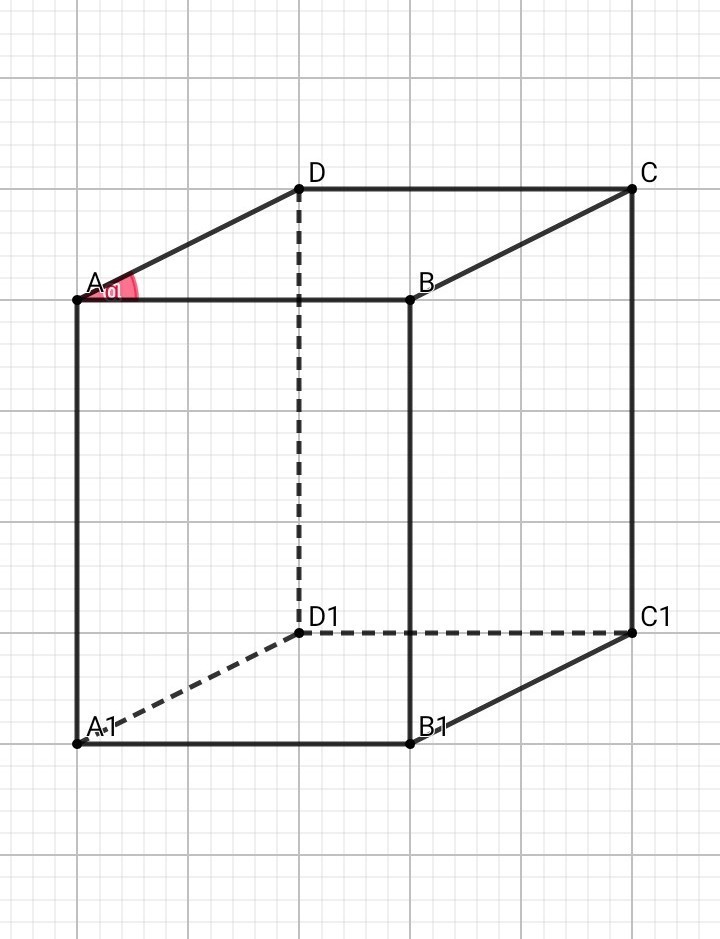
• Рассмотрим параллелограмм АВСD:
Площадь параллелограмма вычисляется по формуле:

$s = a \times b \times sin \alpha$

где а и b - стороны параллелограмма, а - угол между сторонами а и b

S abcd = AB • AD • sin60° = 6 • 8 • V3/2 = 24V3 см^2

• Площадь боковой поверхности прямой призмы вычисляется по формуле:
S бок. = P осн. • h = P abcd • AA1
AA1 = S бок / Р abcd
• Обьём прямой призмы равен:
V = S осн. • h = S abcd • AA1 = S abcd • S бок. / Р abcd = 24V3 • 140 / 28 = 24V3 • 5 = 120V3 см^3


ОТВЕТ: 120V3 см^3