Предмет: Математика,
автор: S1M0PLE
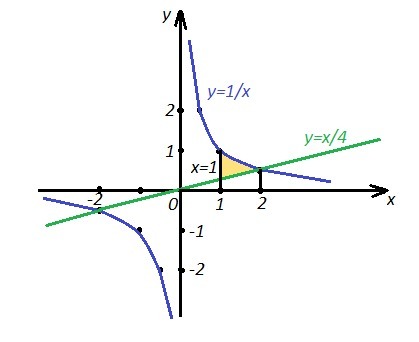
Найти площадь фигуры, ограниченной линиями
y=1/x, y=x/4, x=1
СРОЧНО
Ответы
Автор ответа:
0
Точки пересечения:
Приложения:
Похожие вопросы
Предмет: Обществознание,
автор: Imadevilly
Предмет: Английский язык,
автор: tverdovavlada09
Предмет: Алгебра,
автор: Pushkin220
Предмет: Геометрия,
автор: polinaporayko