Даю 49 баллов.
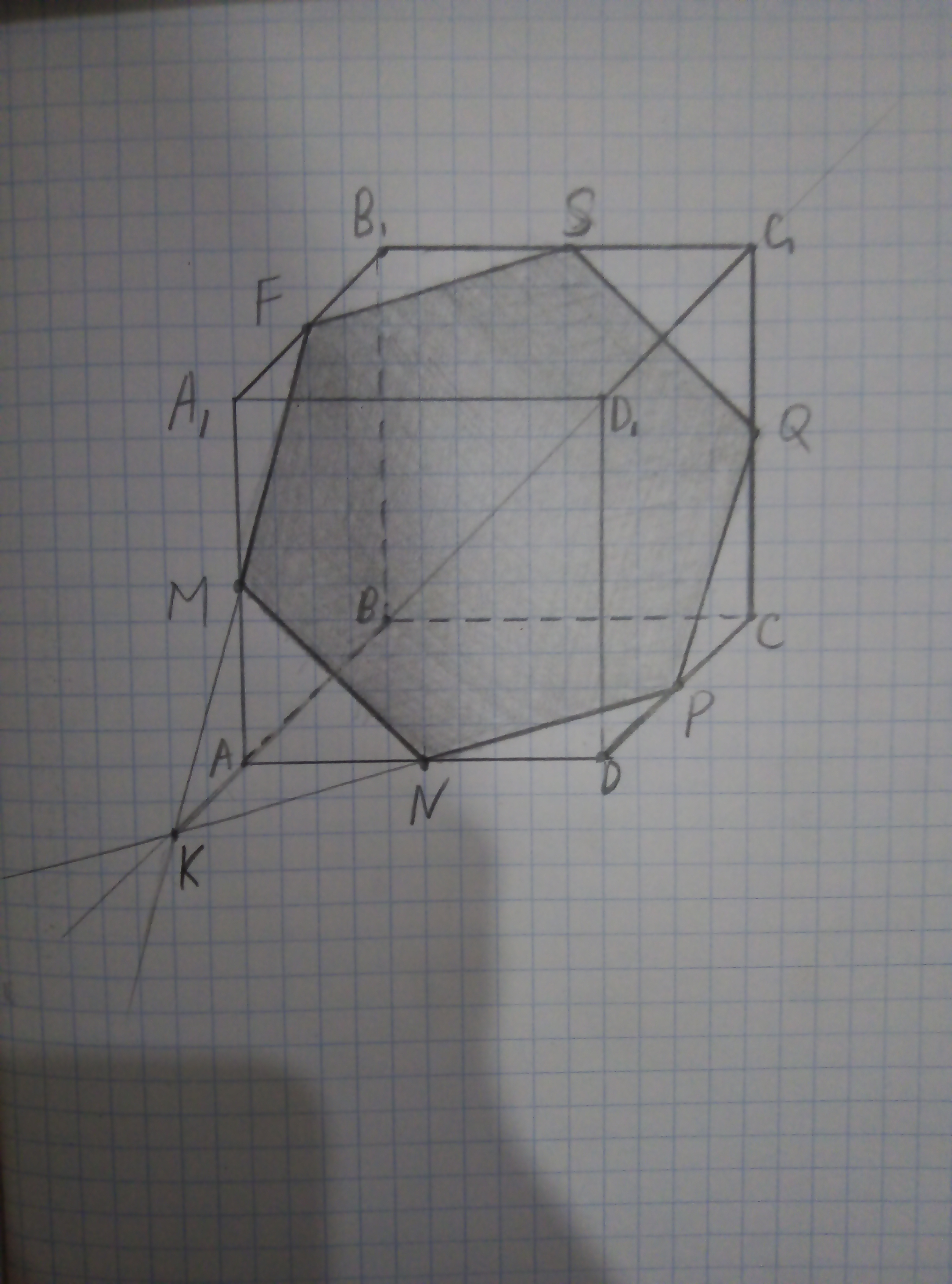
Постройте сечение куба плоскостью, проходящей через три данные точки, являющиеся серединами его рёбер.
Не просто начертите, а объясните ещё, почему Вы провели прямую, например, пожалуйста.

Ответы
Для удобства обозначим куб, как ABCDA₁B₁C₁D₁
1) Соединим точки M и N, а также N и P так как они лежат в одной плоскости (M и N в плоскости AA₁D₁D, N и P в плоскости ABCD)
2) Найдём пересечение прямой NP и плоскости AA₁B₁B. Для этого продолжим прямую NP и прямую AB, до тех пор, пока они не пересекутся. В результате получаем точку K.
3) Через точки K и M проводим прямую, пока не получим пересечения с одним из рёбер в плоскости AA₁B₁B. В результате получаем точку F на ребре A₁B₁
4) Так как грани AA₁B₁B и DD₁C₁C параллельны, через точку P можно провести прямую, параллельную MF. Эта прямая пересечёт ребро CC₁ в точке Q.
5) Аналогично пункту 4 проводим прямую QS || MN, S∈B₁C₁ (т.к. AA₁D₁D || BB₁C₁C)
6) Соединим точки F и S, так как они лежат в одной плоскости A₁B₁C₁D₁.
В результате получаем, что сечением куба ABCDA₁B₁C₁D₁ является шестиугольник NMFSQP.