Предмет: Геометрия,
автор: luiluibuterfly
КТО-НИБУДЬ!!!!!ПРОШУ!!!!!ПОЖАЛУЙСТА!!!! ТОЛЬКО ПУНКТ Б!!!!!
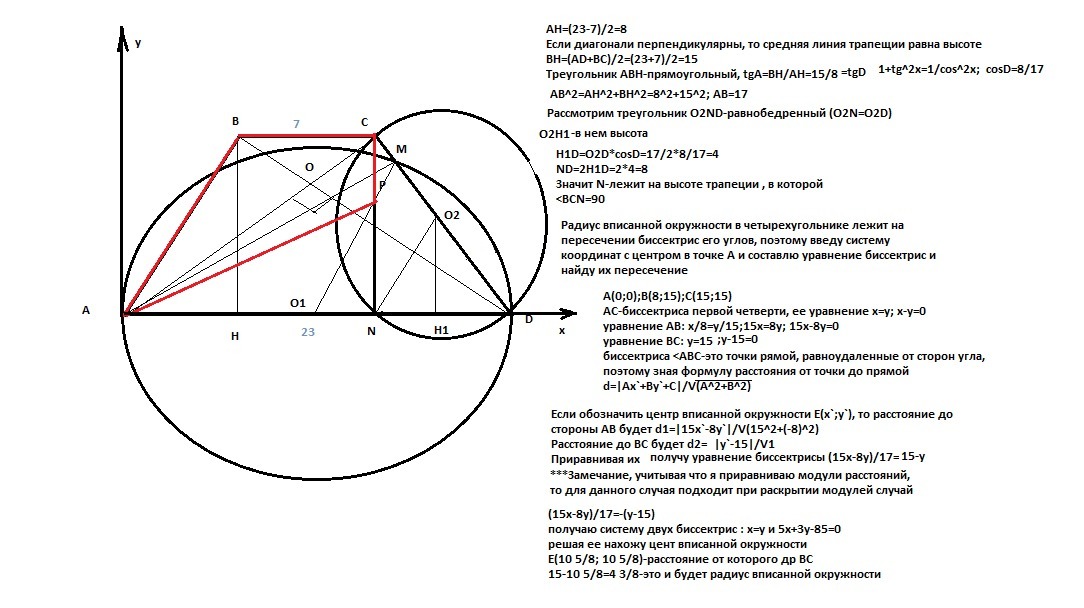
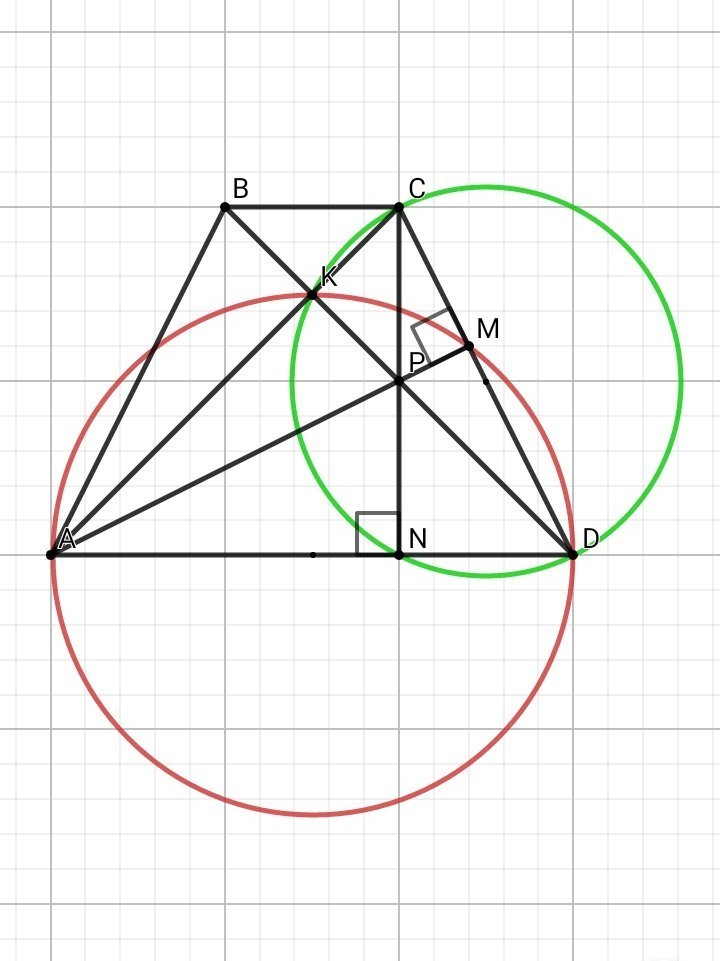
Диагонали равнобедренной трапеции ABCD с основаниями BC и AD перпендикулярны. Окружность с диаметром AD пересекает боковую сторону CD в точке M, а окружность с диаметром CD пересекает основание AD в точке N. Отрезки AM и CN пересекаются в точке P.
а) Докажите, что в четырёхугольник ABCP можно вписать окружность.
б) Найдите радиус этой окружности, если BC=7, AD=23.
ТОЛЬКО Б
luiluibuterfly:
прошу
распишите
почему p лежит на высоте?
пожалуйста!
хотя бы начало
Ответы
Автор ответа:
3
..............................................
Приложения:
спасибо!
огромное!
Автор ответа:
8
РЕШЕНИЕ:
А) • Если в равнобедренной трапеции диагонали взаимно перпендикулярны, то высота данной трапеции равна полусумме оснований =>
СN = ( BC + AD ) / 2 = ( 7 + 23 ) / 2 = 30/2 = 15
• ND = ( 23 - 7 ) / 2 = 16 / 2 = 8
AN = AD - ND = 23 - 8 = 15
• Рассмотрим тр. СND (угол CND = 90°):
По теореме Пифагора:
CD^2 = CN^2 + ND^2 = 15^2 + 8^2 = 225 + 64 = 289
CD = AB = 17
• Рассмотрим тр. АСD:
S acd = ( 1/2 ) • CN • AD
S acd = ( 1/2 ) • AM • CD =>
CN • AD = AM • CD
AM = CN • AD / CD = 15 • 23 / 17 = 345 / 17
• Рассмотрим тр. АСN:
По теореме Пифагора:
АС^2 = СN^2 + AN^2 = 15^2 + 15^2 = 225 + 225 = 450
AC = 15V2 ( V - знак квадратного корня )
• Рассмотрим тр. АСМ:
По теореме Пифагора:
АС^2 = АМ^2 - СМ^2 = ( 15V2 )^2 - ( 345/17 )^2 = 450 - ( 345/ 17 )^2 = 11 025/289
AC = 105/17
• тр. СND подобен тр. СРМ
угол NDC = угол СРМ
sin NDC = CN/CD
sin CPM = CM/CP =>
CN/CD = CM/CP =>
CP = CD • CM / CN = 17 • 105 / 17 • 15 = 105/15 = 7
NP = CN - CP = 15 - 7 = 8
• Рассмотрим тр. АРN:
По теореме Пифагора:
АР^2 = АN^2 + NP^2 = 15^2 + 8^2 = 225 + 64 = 289
AP = 17
• Если в четырёхугольнике сумма противоположных сторон равны, то в этот четырёхугольник можно вписать окружность:
АВ + СР = ВС + АР
17 + 7 = 7 + 17
24 = 24
Значит, в четырёхугольник АВСР можно вписать окружность, что и требовалось доказать.
Б) • Рассмотрим тр. ВСР:
По теореме Пифагора:
ВР^2 = ВС^2 + СР^2 = 7^2 + 7^2 = 49 + 49 = 49 • 2
ВР = 7V2
• Рассмотрим четырёхугольник АВСР:
Если в четырёхугольнике диагонали взаимно перпендикулярны, то её площадь равна половине произведения его диагоналей =>
S abcp = АС • ВР / 2 = 15V2 • 7V2 / 2 = 15 • 7 = 105
• Площадь любого n - угольника рассчитывается по формуле:
S = p • r
где р - полупериметр, r - радиус вписанной окружности

ОТВЕТ: б) 35/8
А) • Если в равнобедренной трапеции диагонали взаимно перпендикулярны, то высота данной трапеции равна полусумме оснований =>
СN = ( BC + AD ) / 2 = ( 7 + 23 ) / 2 = 30/2 = 15
• ND = ( 23 - 7 ) / 2 = 16 / 2 = 8
AN = AD - ND = 23 - 8 = 15
• Рассмотрим тр. СND (угол CND = 90°):
По теореме Пифагора:
CD^2 = CN^2 + ND^2 = 15^2 + 8^2 = 225 + 64 = 289
CD = AB = 17
• Рассмотрим тр. АСD:
S acd = ( 1/2 ) • CN • AD
S acd = ( 1/2 ) • AM • CD =>
CN • AD = AM • CD
AM = CN • AD / CD = 15 • 23 / 17 = 345 / 17
• Рассмотрим тр. АСN:
По теореме Пифагора:
АС^2 = СN^2 + AN^2 = 15^2 + 15^2 = 225 + 225 = 450
AC = 15V2 ( V - знак квадратного корня )
• Рассмотрим тр. АСМ:
По теореме Пифагора:
АС^2 = АМ^2 - СМ^2 = ( 15V2 )^2 - ( 345/17 )^2 = 450 - ( 345/ 17 )^2 = 11 025/289
AC = 105/17
• тр. СND подобен тр. СРМ
угол NDC = угол СРМ
sin NDC = CN/CD
sin CPM = CM/CP =>
CN/CD = CM/CP =>
CP = CD • CM / CN = 17 • 105 / 17 • 15 = 105/15 = 7
NP = CN - CP = 15 - 7 = 8
• Рассмотрим тр. АРN:
По теореме Пифагора:
АР^2 = АN^2 + NP^2 = 15^2 + 8^2 = 225 + 64 = 289
AP = 17
• Если в четырёхугольнике сумма противоположных сторон равны, то в этот четырёхугольник можно вписать окружность:
АВ + СР = ВС + АР
17 + 7 = 7 + 17
24 = 24
Значит, в четырёхугольник АВСР можно вписать окружность, что и требовалось доказать.
Б) • Рассмотрим тр. ВСР:
По теореме Пифагора:
ВР^2 = ВС^2 + СР^2 = 7^2 + 7^2 = 49 + 49 = 49 • 2
ВР = 7V2
• Рассмотрим четырёхугольник АВСР:
Если в четырёхугольнике диагонали взаимно перпендикулярны, то её площадь равна половине произведения его диагоналей =>
S abcp = АС • ВР / 2 = 15V2 • 7V2 / 2 = 15 • 7 = 105
• Площадь любого n - угольника рассчитывается по формуле:
S = p • r
где р - полупериметр, r - радиус вписанной окружности
ОТВЕТ: б) 35/8
Приложения:

Похожие вопросы
Предмет: Математика,
автор: vikafhfh9334
Предмет: Другие предметы,
автор: NastyaKanaeva6473
Предмет: Математика,
автор: russkiyudarnik
Предмет: Алгебра,
автор: Nuraika04