Предмет: Алгебра,
автор: VityaNex
Помогите решить. Нужно упростить.
Приложения:
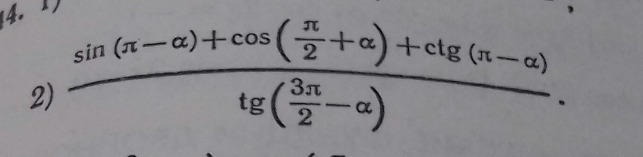
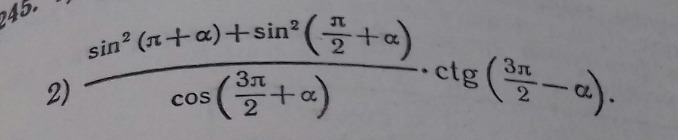
Ответы
Автор ответа:
0
(sin ( n - a) + cos( n/2 + a) + ctg(n-a)) / ( tg 3n/2 - a)= (sin a - sin a - ctg a) / (ctg a) = -ctg a/ ctg a= -1
((sin²(n+a)+sin²(n\2+a)) / (cos(3n/2+a)) * ctg(3n/2-a) = ((sin² a +cos²)/sin a) * tg a = (1/sin a)*(sin a/cos a) = 1/cos a
Автор ответа:
0
Похожие вопросы
Предмет: Қазақ тiлi,
автор: aesimgozin24
Предмет: Русский язык,
автор: audia6794
Предмет: Русский язык,
автор: huseynlicimnaz217
Предмет: Математика,
автор: Аноним
Предмет: Литература,
автор: катя2687