Предмет: Геометрия,
автор: Sarafanova1
Точка М лежит на окружности радиуса R, описанной около прямоугольника ABCD.
Докажите, что МА^2+ МВ^2+ МС^2+ МD^2= 8R^2
Ответы
Автор ответа:
2
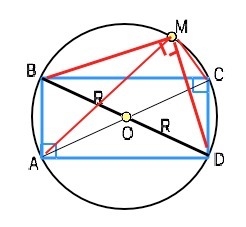
АВСD – прямоугольник, его диагонали – диаметры описанной окружности. ⇒ угол М в треугольниках ВМD и АМС - прямой. В ∆ АМС по т.Пифагора MA²+MC²=BD²; в ∆ BMD по т.Пифагора МВ²+МD²=BD²
Сложив два уравнения, получим. МА²+МВ²+МС²+МD²=2BD² Диаметр DВ=2R, следовательно, 2BD²=2(2R)²=8R² ⇒ МА²+МВ²+МС²+МD²=8BD² Доказано.
Приложения:
Похожие вопросы
Предмет: Литература,
автор: Аноним
Предмет: Русский язык,
автор: assasincorvo455
Предмет: Английский язык,
автор: shockhacker64
Предмет: Геометрия,
автор: Katyalee888