Question

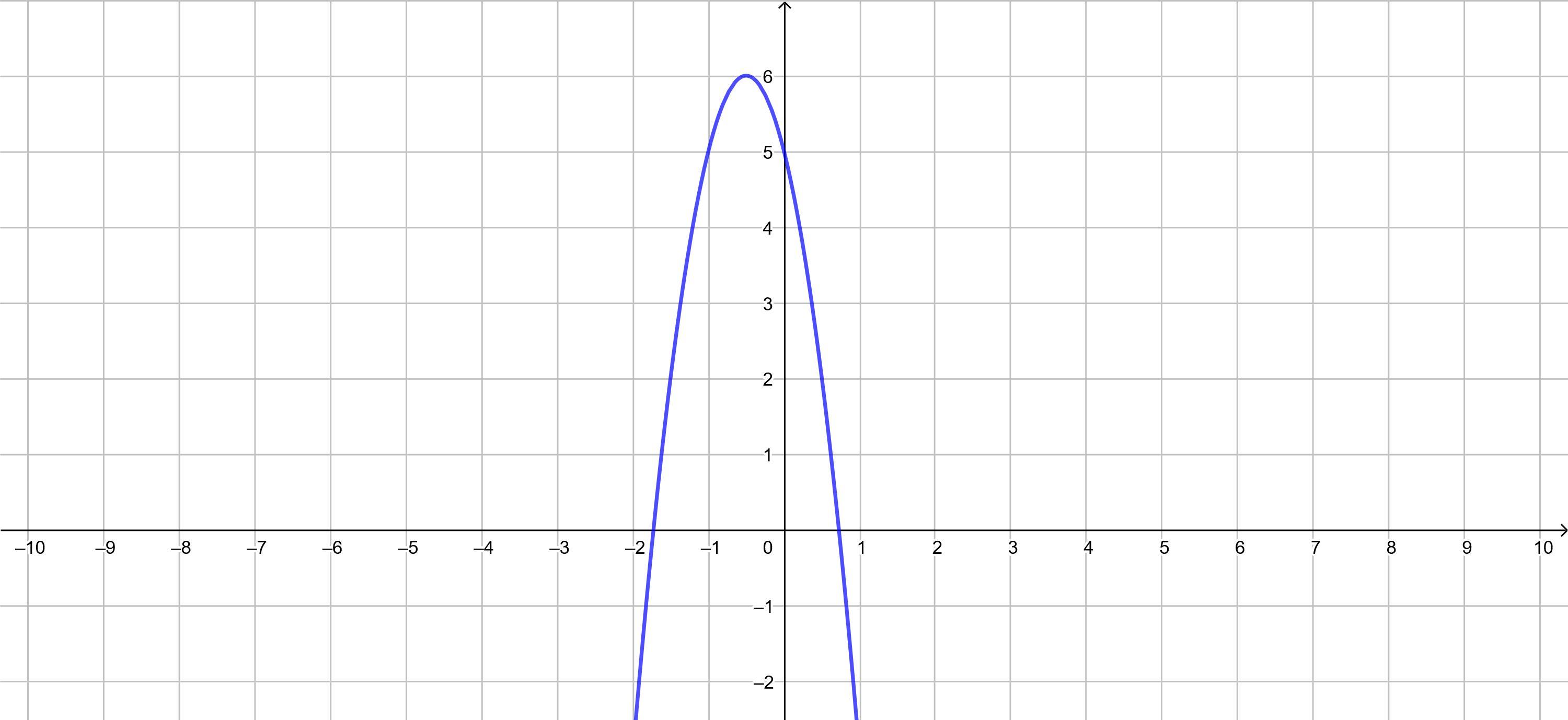
Найдите точки максимума и минимума функции f(x)=5-4x-4x^2

Answer 1

1. Запишем функцию в стандартном виде.

Данная функция - квадратичная (функция, уравнение которой включает в себя переменную ${x}^{2}$). Стандартный вид функции: $f(x)=a{x}^{2}+bx+c$.

То есть в нашей функции $5$ это $c$, $-4x$ это $bx$ и $-4{x}^{2}$ это $a{x}^{2}$.

• Стандартный вид функции: $f(x)=-4{x}^{2}-4x+5$.

2. Определим направление параболы.

График квадратичной функции - парабола (геометрическое место точек, равноудалённых от данной прямой). Ветви параболы могут быть направлены вверх и вниз.

Если коэффициент $a$ при переменной ${x}^{2}$ положительный, то ветви параболы направлены вверх. Если же коэффициент отрицательный, то ветви параболы направлены вниз.

• $f(x)=-4{x}^{2}-4x+5$. Здесь $a=-4$, поэтому ветви параболы направлены вниз.

3. Вычислим координату $x$ вершины параболы.

Координата $x$ вершины параболы - значение $-(b/2a)$. Если квадратичная функция записана в стандартном виде $a{x}^{2}+bx+c$, воспользуемся коэффициентами $x$ и ${x}^{2}$:

• В функции $f(x)=-4{x}^{2}-4x+5$ коэффициенты $a=b=-4$. Т.е. координата $x$ вершины параболы: $x = -\Big((-4)/(-8)\Big)=-1/2$.

4. Найдём соответствующее значение $f(x)$.

Мы ищем максимум функции, так как ветви параболы направлены вниз. Чтобы найти максимум нужно подставить в исходную функцию $f(x)=-4{x}^{2}-4x+5$ найденное значение $x$.

• $f(x)=f(-1/2)=-4\cdot{(-1/2)}^{2}-4\cdot(-1/2)+5=6$

5. Запишем окончательный ответ.

Точка максимума функции равна $6$.