Предмет: Алгебра,
автор: rrrrrbldgkb
тригонометрия. 63-66.
Приложения:
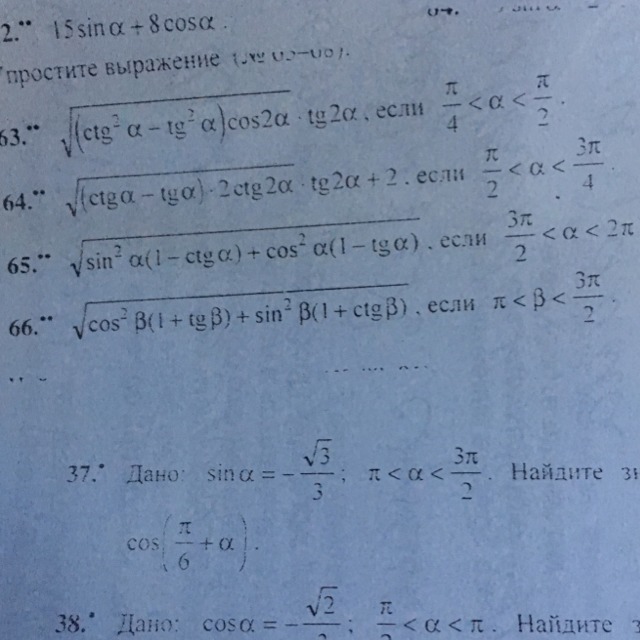
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Информатика,
автор: turalabbasov2004
Предмет: Алгебра,
автор: mashasolodovad
Предмет: Математика,
автор: androsila656
Предмет: Алгебра,
автор: ivan3341
Предмет: Геометрия,
автор: voldemortnukus12