Предмет: Алгебра,
автор: ShkolyarVanya
 Помогите пожалуйста!!!!производная
Помогите пожалуйста!!!!производная
Ответы
Автор ответа:
1
решение на фотографии
Приложения:
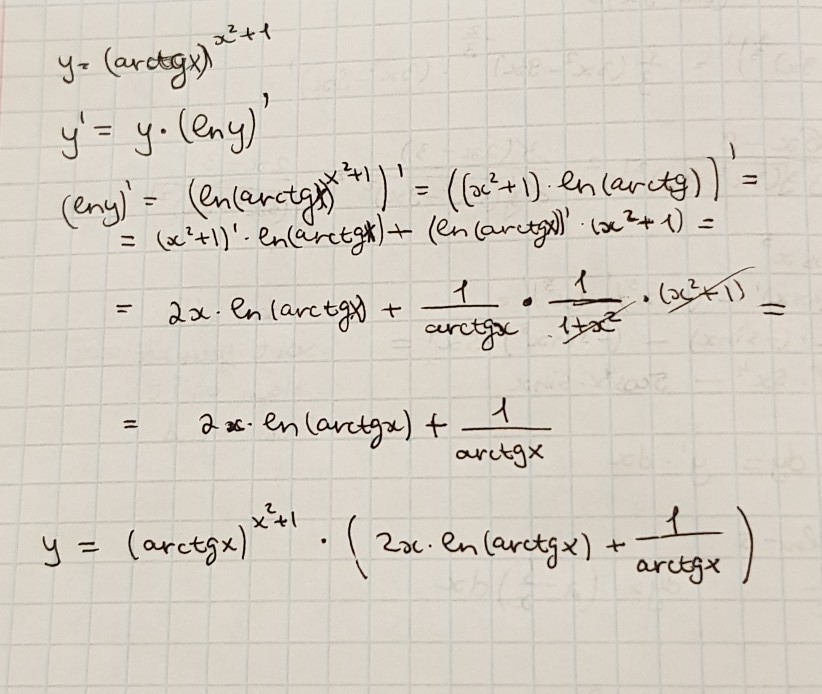
Автор ответа:
1
прологарифмируем функцию:
Похожие вопросы
Предмет: Алгебра,
автор: frommoscowmosc8
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Математика,
автор: ergalievruslan
Предмет: Физика,
автор: бродяга23