Question

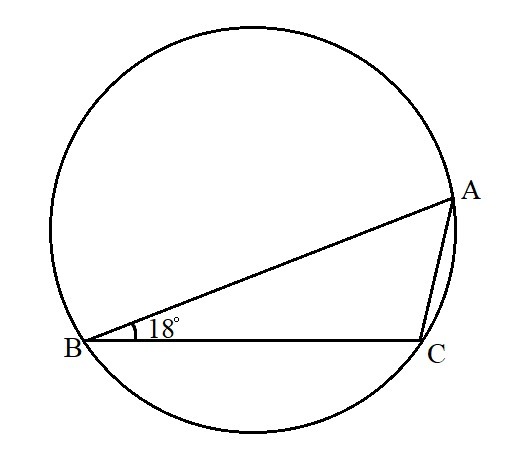
Треугольник АВС вписан в окружность, угол АВС равен 18°. Найдите длину дуги АС, если произведение радиуса этой окружности и числа π равно 10.

Answer 1

Так как ∠ABC - вписанный, дуга AC = 2∠ABC = 36°.

Длина окружности $l=2\pi R$. Так как $\pi R=10$, то $2\pi R=l=20$.

Длина дуги $L=\frac{\alpha}{360\textdegree}l=\frac{36\textdegree}{360\textdegree}*20=\frac{20}{10}=2$

Ответ: 2