Предмет: Математика,
автор: 0007инкогнет0007
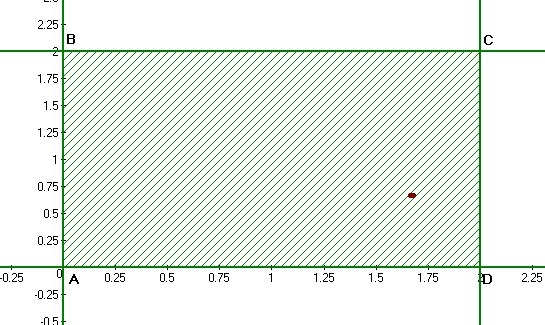
Найти наибольшее и наименьшее значения функции  в области D: x=0,x=2,y=0,y=2. (Надо исследовать функцию на границах области и на угловых точках) Напишите подробное решение
в области D: x=0,x=2,y=0,y=2. (Надо исследовать функцию на границах области и на угловых точках) Напишите подробное решение
Ответы
Автор ответа:
0
Данная точка входит в область D, поэтому находим значение в точке.
Теперь проверяем границы.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: vasilisadegteryova
Предмет: Английский язык,
автор: anastasiacufarliceva
Предмет: Русский язык,
автор: flexor
Предмет: Математика,
автор: Limon989
Предмет: Алгебра,
автор: pashakononenko