Предмет: Математика,
автор: shitanyway
логарифмы. нужно упростить. даю много
Приложения:
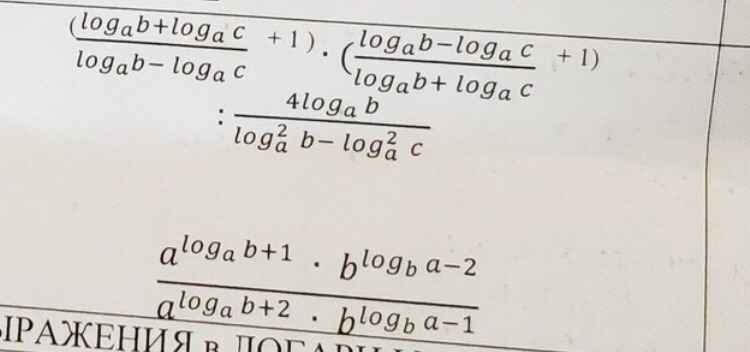
Ответы
Автор ответа:
0
чтобы проще работать введем обозначения log b поосн.а=х, log c по осн а=у, тогда(x+y/x-y +1)*(x-y/x+y +1)*(x-y)(x+y)/4x=x+y+x-y/x-y +x+y/x+y *(x-y)(x+y)/4x=4x^/4x=x=logb по осн.а
(b+1)(a-2)/(b+2)(a-1) это ответ ко 2-му
Автор ответа:
1
1)
2)
Похожие вопросы
Предмет: Физика,
автор: mariyachernykh86
Предмет: География,
автор: cupcake28
Предмет: Алгебра,
автор: didievavalentina
Предмет: Математика,
автор: обезьянкацыцыцы
Предмет: Математика,
автор: mila260703