Question

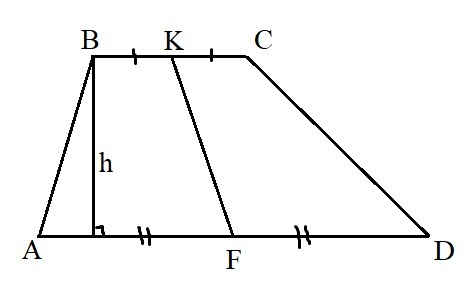
В трапеции ABCD точки F и K - середины оснований АD и BC соответственно.Докажите,что площадь трапеции ABFK равна половине площади трапеции ABCD.

Answer 1

$S_{ABCD}=\frac{(AD+BC)}{2}h\\ S_{ABKF}=\frac{AF+BK}{2}h=\frac{\frac{AD}{2}+\frac{BC}{2}}{2}h=\frac{\frac{AD+BC}{2}}{2}h=\frac{AD+BC}{4}h=\frac{AD+BC}{2}h:2=\\=S_{ABCD}:2$

Отсюда площадь трапеции ABKF равна половине площади трапеции ABCD, что и требовалось доказать.