Предмет: Математика,
автор: iskyzhin2004
Докажите пожалуйста.
Приложения:
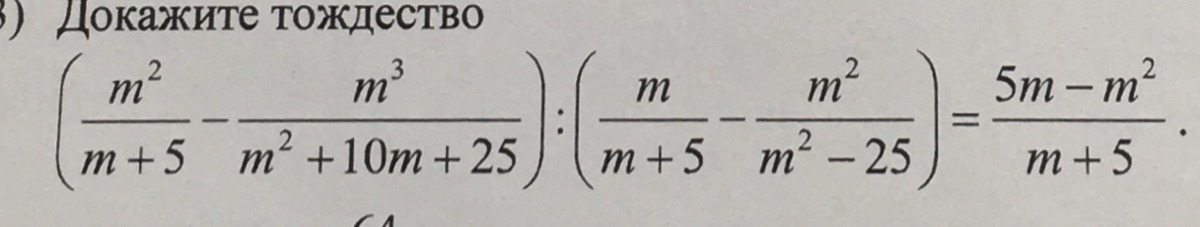
Ответы
Автор ответа:
1
Доказать тождество.
Что и требовалось доказать.
Похожие вопросы
Предмет: История,
автор: MrSnowJK
Предмет: Биология,
автор: abdullaharziev08
Предмет: Математика,
автор: viktorfilippov637
Предмет: Химия,
автор: zaharbibikov