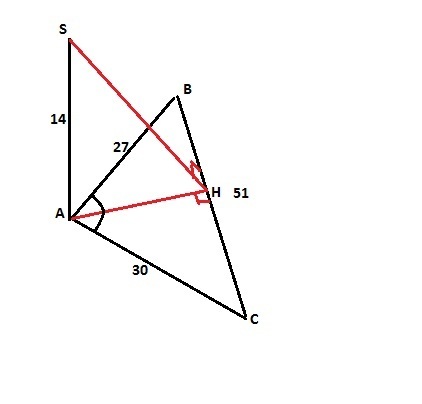
из вершины большего угла треугольника к его плоскости проведён перпендикуляр равный 14см. Определить расстояние от концов перпендикуляра до противолежащей стороны треугольника, стороны которого равны 27см, 30см, 51см
даю 70 баллов за быстрое решение.
Ответы
В треугольнике АВС против большей стороны лежит больший угол (свойство). Проведем перпендикуляр АН из большего угла А на его большую сторону ВС. Это высота треугольника АВС. Найдем эту высоту. Есть два варианта: 1) найти площадь по формуле Герона и затем - высоту, проведенную к стороне 51 см. 2) выразить эту высоту уравнениями из прямоугольных треугольников САН и ВАН по Пифагору и затем найти высоту, приравняв оба уравнения и учтя, что СН = х, а ВН = (51-х). Возьмем первый вариант, так как он сразу выводит нас на искомую высоту. Полупериметр треугольника равен р=(27+30+51)/2 = 54см. Тогда по формуле Герона:
Sabc = √(54*27*24*3) = 324 см². Так как S=(1/2)*BC*AH, находим АН: АН=2S/BC = 648/51 ≈ 12,7 см (за приблизительный ответ виновен составитель задачи).
Итак, мы нашли расстояние от основания перпендикуляра до противоположной стороны треугольника. Расстояние от вершины перпендикуляра до этой же стороны найдем по Пифагору из прямоугольного треугольника SAH (S - вершина перпендикуляра к плоскости АВС, а SH - перпендикуляр к ВС по теореме о трех перпендикулярах): SH=√(14²+12,7²) ≈ 18,9 cм.
Ответ: искомые расстояния равны 12,7 см и 18,9 см.