Предмет: Алгебра,
автор: Lovatic2602
Помогите пожалуйста.
Приложения:
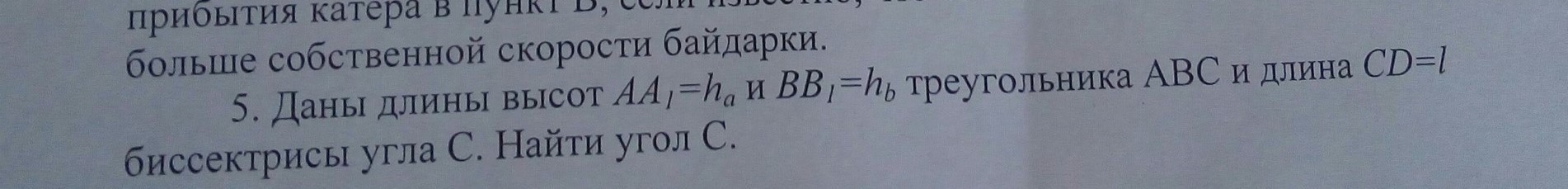
Ответы
Автор ответа:
1
Имеем: . Остается воспользоваться формулой для длины биссектрисы
. Подставив вместо a и b выписанные выражения, получаем
Ответ:
Замечание. Мы имели право писать, что C/2 равен арксинусу, поскольку C/2 лежит в первой четверти.
Lovatic2602:
Огромное спасибо!
Похожие вопросы
Предмет: История,
автор: makaryurchenko2012
Предмет: Физика,
автор: Stalkker228g
Предмет: Математика,
автор: applelehan90
Предмет: Математика,
автор: Галя12345ру