Предмет: Алгебра,
автор: Lovatic2602
Помогите пожалуйста решить систему уравнений
Приложения:
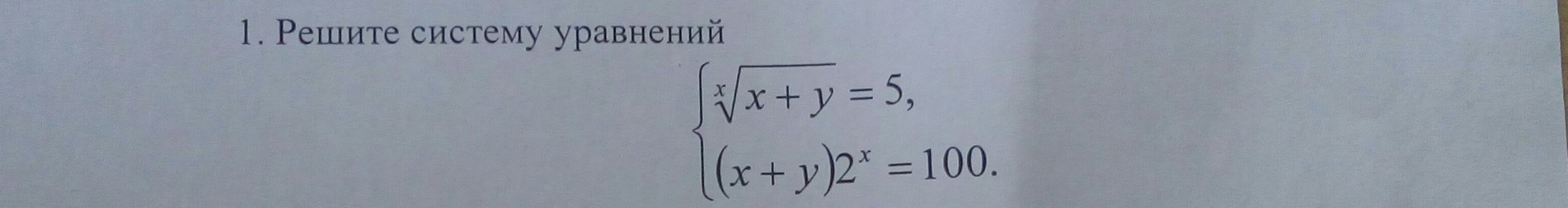
Ответы
Автор ответа:
1
Извлечём из второго уравнения корень степени "х":
Учитывая первое уравнение получим:
При одинаковых основаниях, выражения будут равны, если равны их степени.
Подставим полученное значение х во второе уравнение.
Подставив полученный ответ в исходные уравнения обнаружим, что всё выполняется.
Таким образом, ответ: (2; 23).
Lovatic2602:
Большое спасибо!
Автор ответа:
1
Решение на фотографии.
Приложения:

Спасибо!
Пожалуйста!
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: agafonovapolina472
Предмет: Литература,
автор: margaritaklejnsbergs
Предмет: Алгебра,
автор: nastyaa261199