Предмет: Математика,
автор: normdich
нужно решить 1 и 2 пример
Приложения:
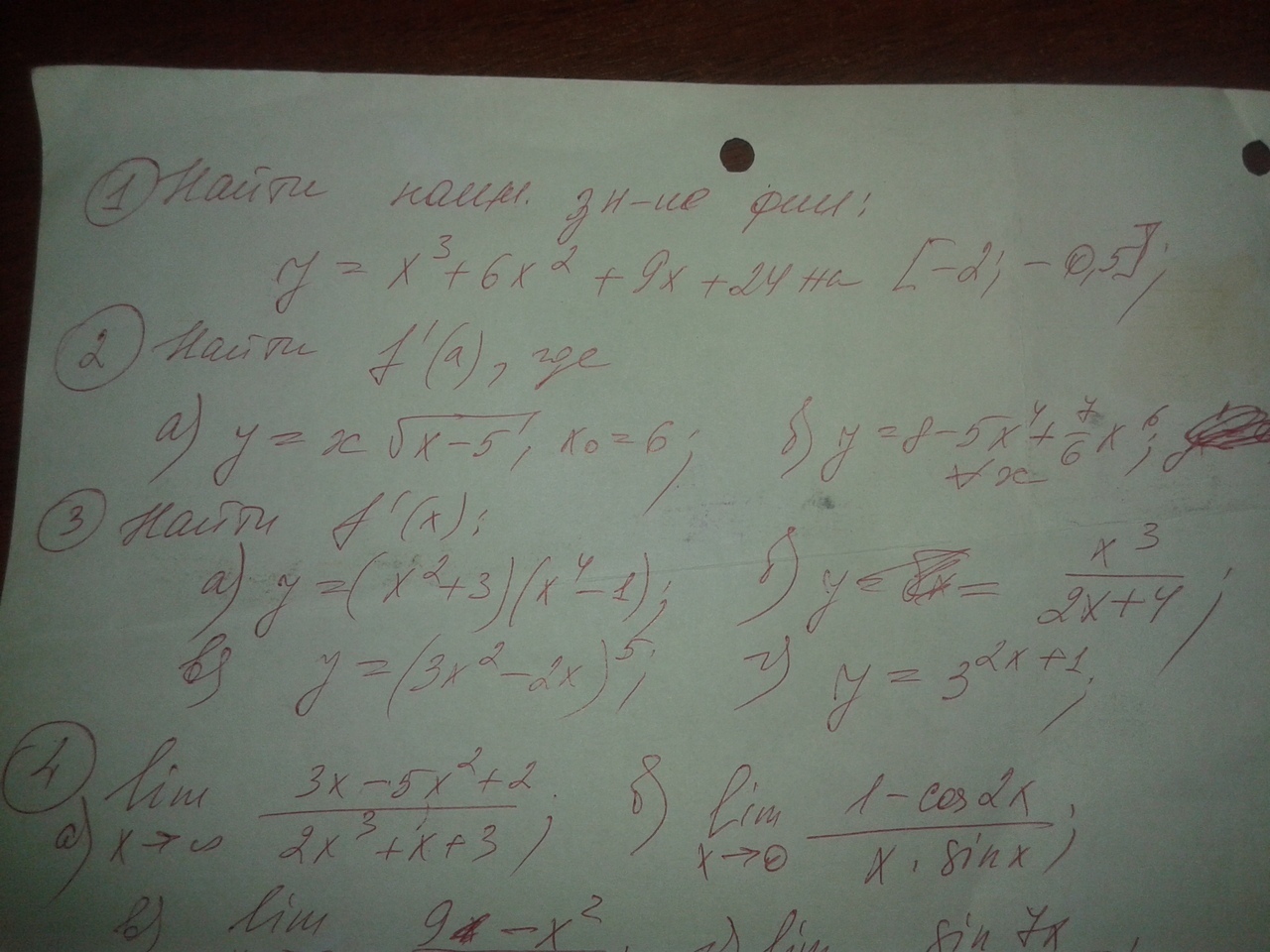
Ответы
Автор ответа:
1
1. Точки местных максимумов и минимумов определяются нулями первой производной
f'(x) =3x²+12x+9
Решаем x²+4x+3=0
Перепишем в виде
(x+3)(x+1)=0
Корни x=-3, x=-1
Поскольку график f(x) это кубическая парабола, которая возрастает на участках от - бесконечности до -3 и от -1 до бесконечности, а уменьшается на участке от -3 до -1 , то местный минимум f(x) будет в точке x=-1, где f(x) принимает значение
-1+6-9+24=20
Таким образом точка минимума функции на участке [-2;-0,5] это (-1; 20)
2.а) f(x) =x\/(x-5)
f'(x) =\/(x-5) + x/[2\/(x-5)]
б) f(x) =8-5x⁴+7/6x^6
f'(x) =-20x³+7x^5
normdich:
аа!эээ спасибо!
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: sasanna450
Предмет: Русский язык,
автор: egoregorov7364
Предмет: Алгебра,
автор: макс1810
Предмет: Геометрия,
автор: Speak123