Предмет: Алгебра,
автор: 55555ученик55555
log3(sin (2x))=log3(cos(x))
Ответы
Автор ответа:
1
I hope this helps you
Приложения:
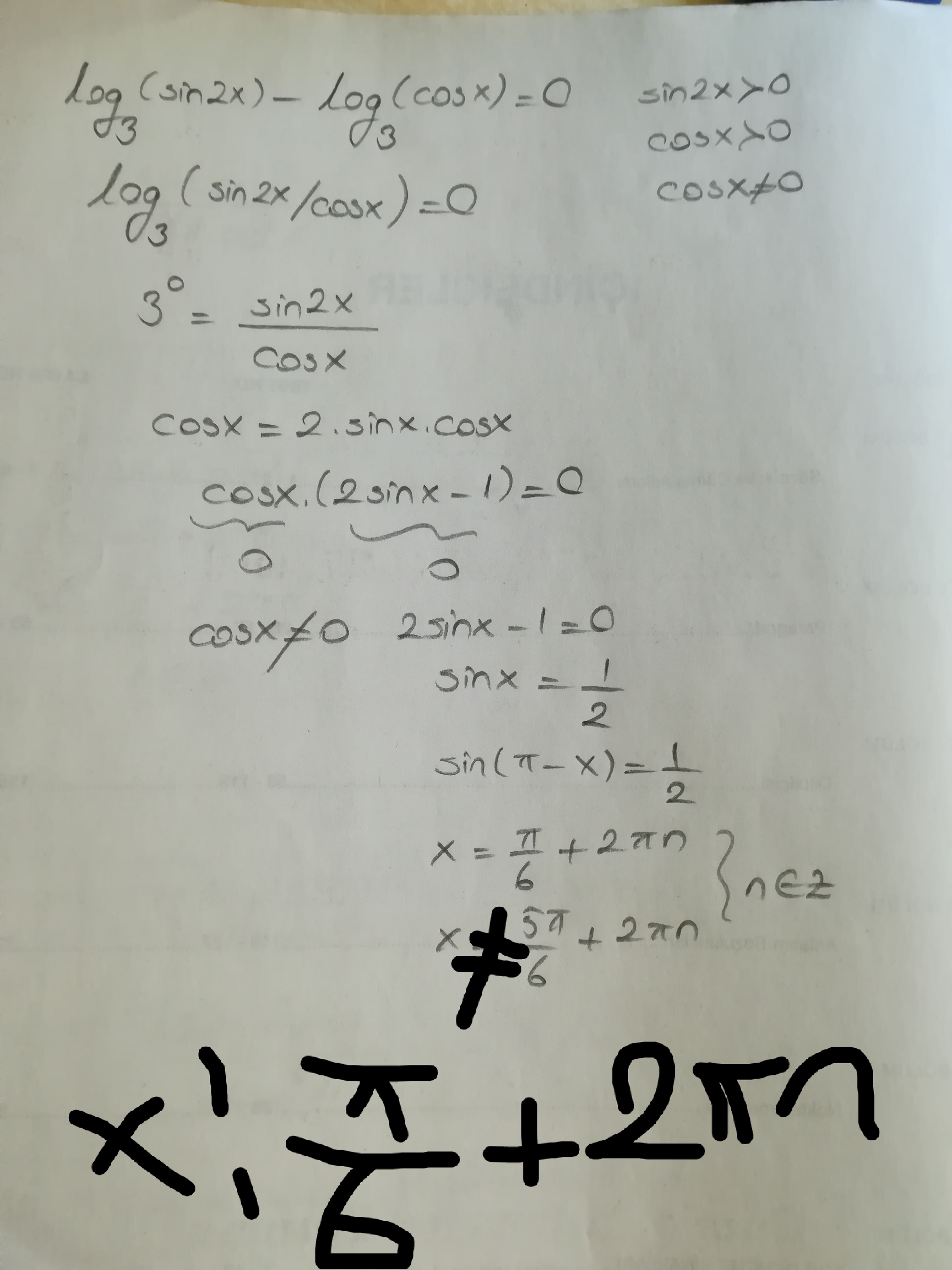
55555ученик55555:
а 5pi/6 + 2pi не следует исключать?
следует, конечно
sorry i wasn't online :/
Автор ответа:
1
ОДЗ: sin2x>0 и cosx>0 ⇒ x ∈ I четверти тригонометрического круга (края выколоты)
Ответ: x=π/6+2πk; k∈Z
Похожие вопросы
Предмет: Українська література,
автор: Sed243
Предмет: Алгебра,
автор: raevskiyruslan09
Предмет: Биология,
автор: lochgipon
Предмет: Алгебра,
автор: merci0077
Предмет: Математика,
автор: jarkob