Предмет: Алгебра,
автор: Данякеп
Решите производную.....
Приложения:
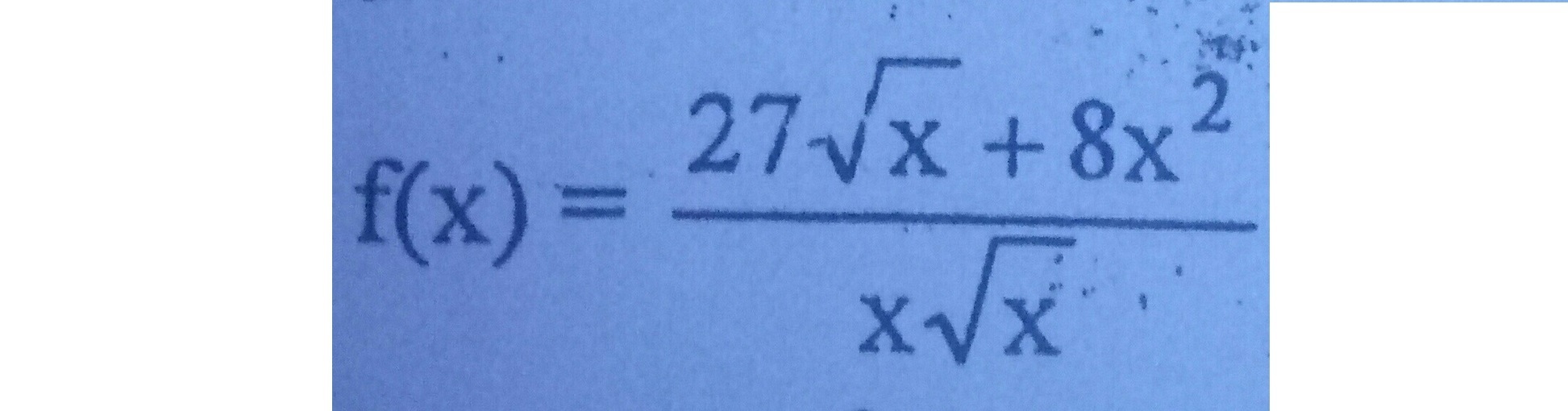
Ответы
Автор ответа:
1
решение во вложении:
Приложения:

xxxeol:
ПРавильно.
Автор ответа:
1
Похожие вопросы
Предмет: Алгебра,
автор: zuleyb
Предмет: Алгебра,
автор: blackstic1
Предмет: Русский язык,
автор: albinka1396
Предмет: Физика,
автор: olya300