Предмет: Алгебра,
автор: Данякеп
Решите производную.....
Приложения:
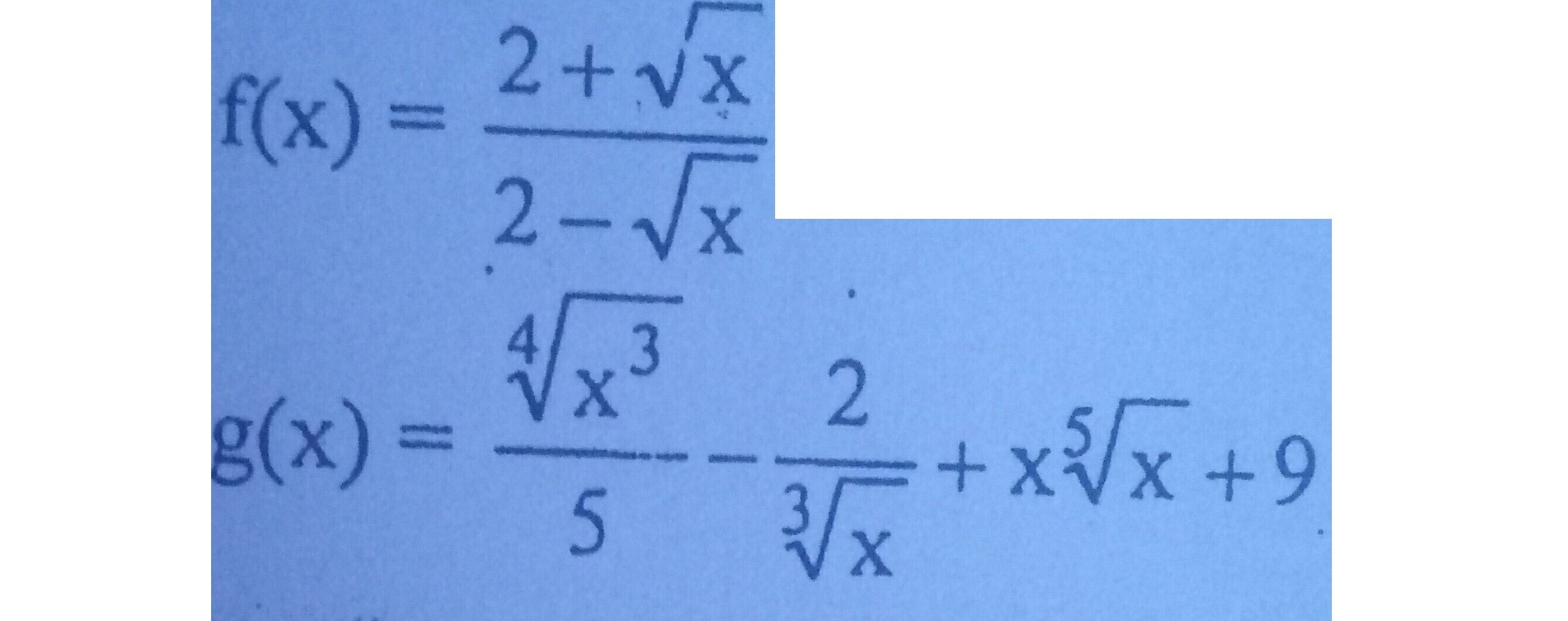
Ответы
Автор ответа:
2
Сначала функция g(x) - полином.
ПРАВИЛО: Производная суммы равна сумме производных.
Записываем функцию g(x) в виде полинома - в степенях.
g(x) = 1/5*x³/⁴ - 2*x⁻¹/³ + x⁶/⁵
Теперь дифференцируем степени - важно не ошибиться.
g'(x) = (1/5*3/4)*x⁻¹/⁴ - (2*-1/3)*x⁻⁴/³ + (6/5)*x¹/⁵
Пробуем записать в виде радикалов.
Функцию f(x) можно записать как произведение двух функций. (Можно как и частное).
f(x) =u(x)*v(x) = (2+√x) * (2-√x)⁻¹
Правило дифференцирования: f'(x) = u'(x)*v(x) + v'(x)(*u(x).
Запись уравнения на рисунке в приложении.
Приложения:
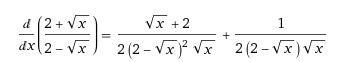
Похожие вопросы
Предмет: Українська література,
автор: teleginmaksim758
Предмет: Литература,
автор: e11na
Предмет: Геометрия,
автор: Аноним
Предмет: Математика,
автор: Nasty5555
Предмет: Алгебра,
автор: happyjhfxx