Предмет: Алгебра,
автор: moetyan
Ребят мне очень срочно!!!!
Найти общее решение( или общий интеграл) дифференциального уравнения с разделяющимися переменными:
Приложения:
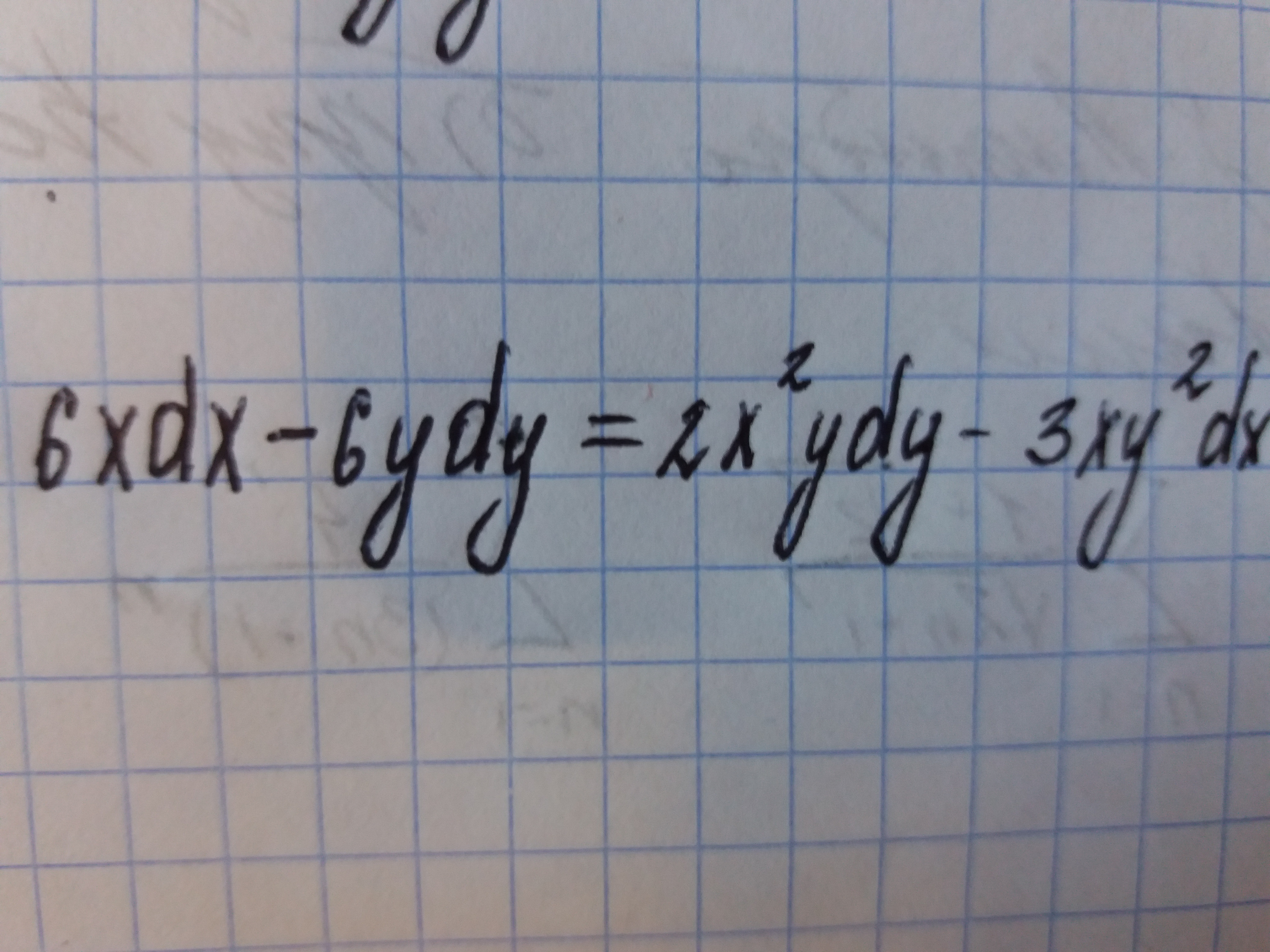
Ответы
Автор ответа:
1
moetyan:
Вы мой спаситель, помогите с крайним: https://znanija.com/task/30249523
Похожие вопросы
Предмет: Русский язык,
автор: klockovaroslav188
Предмет: Обществознание,
автор: Riotik23
Предмет: Информатика,
автор: SklMatt
Предмет: Алгебра,
автор: вероника508
Предмет: Математика,
автор: Marmeladka398