Question

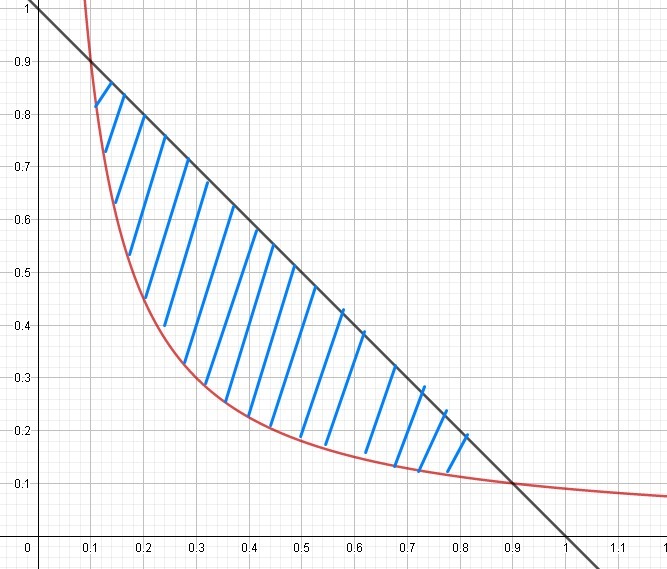
Наудачу взяты два положительных числа х и у, каждое из которых не превышает 1. Найти вероятность того, что сумма х+у будет не больше 1, а произведение xу не меньше 0.09

Answer 1

Эта задача на геометрическую вероятность....

Найдем для начала площадь заштрихованной фигуры:

$\sf S=\displaystyle \int\limits^{0.9}_{0.1}{\bigg(1-x-\frac{0.09}{x}\bigg)} \, dx=\bigg(x-\frac{x^2}{2}-0.09\ln x\bigg)\bigg|^{0.9}_{0.1}=0.9-\frac{0.81}{2}-\\ \\ -0.09\ln0.9-0.1+\frac{0.01}{2}+0.09\ln 0.1=0.8-0.4+0.09\ln\frac{0.1}{0.9}=\\ \\ =0.4+0.09\cdot(-2)\cdot \ln 3=0.4-0.18\ln 3$

Вероятность того, что сумма х+у будет не больше 1, а произведение ху не меньше 0,09, равна:

$\sf \displaystyle P=\frac{S}{L\left([0;1]\times [0;1]\right)}=\frac{0.4-0.18\ln 3}{1}=0.4-0.18\ln 3\approx 0.2$