Предмет: Алгебра,
автор: nika9760
помогите пожалуйста!!!
не будьте равнодушны
Приложения:
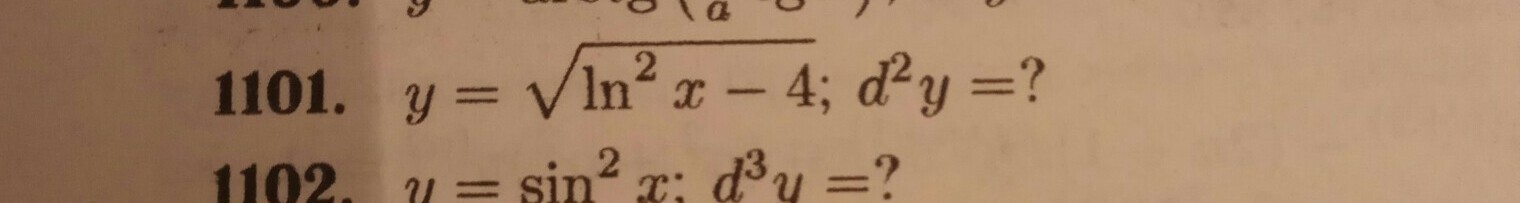
vahe2907:
Что за d^2?
дифференциал
это не имеет значения
главное найти производную
вторую производную
Хорошо, сейчас попробуем найти производную
Ответы
Автор ответа:
2
Как-то так))
спасибо
это только первая производная
Надо вторую произовдную?
производную*
ага ))
Аааа, ну ок)
Похожие вопросы
Предмет: Математика,
автор: edgarosipov07
Предмет: Музыка,
автор: alenamoskaleva2020
Предмет: ОБЖ,
автор: ekuzmina127
Предмет: Химия,
автор: СашаШайн
Предмет: Физика,
автор: Мурат1997