Question

Помогите пожалуйста, срочно!
(x^2+6x-7)/(x+1)
1) Найдите критические точки
2) Асимптомы
3)Точки перегибы, интервалы выпуклости

Answer 1

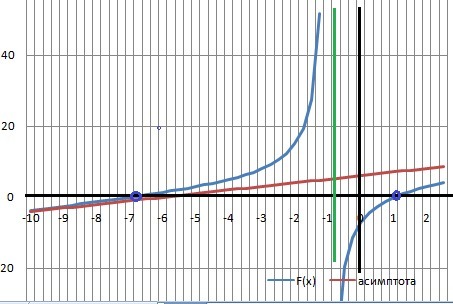
ДАНО: (x² + 6*x - 7)/(x+1).

ИССЛЕДОВАНИЕ.

1. Область определения. В знаменателе = х + 1 ≠ 0 и х ≠-1.

Разрыв при Х= -1.  X∈(-∞;-1)(-1;+∞)

Вертикальная асимптота - Х = - 1.

2. Пересечение с осью Х.

x² + 6*x - 7 = (x-1)*(x+7) = 0

x1 = - 7,  x2 = 1  

2. Первая производная.

$y'(x) = \frac{2x+6}{x+1}- \frac{x^2+6*x-7}{(x+1)^2}=0$

Корней - нет, экстремумов - нет.

Возрастает везде, где существует.

3. Вторая производная.

$y"(x)=\frac{2}{x+1}- \frac{2*(2x-6)}{(x+1)^2}+ \frac{2*(x^2+6x-7)}{(x+1)^3}=0$

Корней - нет, точек перегиба - нет.

Вогнутая - Х∈(-∞;-1), выпуклая - Х∈(-1;+∞)

4. Наклонная асимптота -

$\lim_{x \to \infty}\frac{x^2+6*x-7}{x*(x+1)}=x+6$

y = x + 6 - асимптота

5. График в приложении.